Question

A triangle has corners at `(5 ,7 )`, `(2 ,1 )`, and `(1 ,6 )`. What is the area of the triangle's circumscribed circle?

Answer 1

Area of circumcircle `A_c = 35.5878`

Explanation:

`M_3 = (5+2)/2, (7+1)/2 = (7/2, 4)`

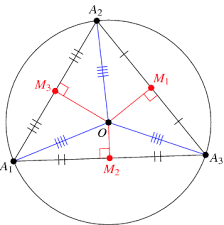
Slope of A1A2 = (7-1)/(5-2) = 2#

Slope of perpendicular bisector thro `M_3= -1/2`

Equation of perpendicular bisector through `M_3` is

`y - 4 = (-1/2) (x - (7/2))`

`4y - 16 = -2x + 7`

`4y + 2x = 23` Eqn (1)

`M_1 = (2+1)/2, (1+6)/2 = (3/2, 7/2)`

Slope of A2A3 = (6-1) / (1-2) = -6#

Slope of perpendicular bisector through `M_1 = -1/-6 = 1/6`

Equation of perpendicular bisector through `M_1` is

`y - (7/2) = (1/6) (x - (3/2))`

`12y - 42 = 2x - 3`

`12y - 2x = 39` Eqn (2)

Solving equations (1), (2) we get coordinates of circumcenter O.

`O (15/4, 31/8)`

Circumcircle radius `R_o = sqrt(((15/4)-2)^2 + ((31/8) - 1)^2) = 3.3657`

Area of circumcircle `A_c = pi R_o^2 = pi * (3.3657)^2 = 35.5878`

Answer 2

Circumcircle area `= {1105 pi}/98`

Explanation:

I worked out the general case here .

I'm going to ignore the details of the general answer, and state the main result as: The squared radius of the circumcircle equals the product of the squared sides of the triangle divided by sixteen times the squared area of the triangle. Given triangle with sides `a,b,c` and area `A`, the circumradius `r` satisfies

`r^2 = {a^2b^2c^2}/{16A^2}`

It's tempting to take the square root, but experience shows much smoother sailing if we don't. We can get the area from the coordinates using the Shoelace Theorem, or get `16A^2` directly from the squared sides using Archimedes' Theorem:

`16A^2 = 4a^2b^2 - (c^2-a^2-b^2)^2`

Since we need the squared sides for the numerator anyway, let's do it this way. We'll label the vertices `A(5,7),` `B(2,1),` `C(1,6)` and calculate

`a^2 = BC^2 = (2-1)^2+(1-6)^2=1^2+5^2=26`

`b^2 = AC^2 = 4^2+1^2=17`

`c^2 = AB^2 = 3^2+6^2=45`

`16 A^2 = 4(26)(17)-(45-26-17)^2 = 1764`

# r^2 = {a^2b^2c^2}/{16A^2} = { (26)(17)(45) }/ 1764 = 1105/98 #

Circumcircle area `= pi r^2 = {1105 pi}/98`