Question

A triangle has corners at points A, B, and C. Side AB has a length of `18`. The distance between the intersection of point A's angle bisector with side BC and point B is `3`. If side AC has a length of `20`, what is the length of side BC?

Answer 1

`6 1/3" units"`

Explanation:

`"let D be the point on BC where the angle bisector"`
`"intersects BC"`

`"using the "color(blue)"angle bisector theorem"`

`color(red)(bar(ul(|color(white)(2/2)color(black)((AB)/(AC)=(BD)/(DC))color(white)(2/2)|)))larrcolor(blue)"to find DC"`

`rArr18/20=3/(DC)`

`rArrDC=(3xx20)/18=20/6=3 1/3larrcolor(blue)"cross-multiplying"`

`rArrBC=BD+DC=3+3 1/3=6 1/3" units"`

Answer 2

Length of `BC = color(red)(19/3)`

Explanation:

Given : side AB = c = 18, BD = 3 & AC = 20.

To find BC.

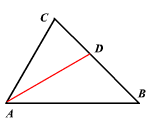
As per angular bisector theorem,

`(AB) / ( AC) = (BD) / (DC)`

`:. DC = (BD * AC) / (AB) = (3 * 20) / 18 = 10/3`

But `BC = BD + DC = 3 + (10/3) = 19/3`