Let us consider a right angled triangle in general and an incircle within it as shown below.
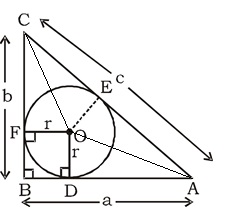
Observe that centre of incircle #O# makes three triangles with sides #a#, #b# and #c# and as area of triangle is #1/2xx"base"xx"height"# #-# and hence area of these triangles is #(ar)/2#, #(br)/2# and #(cr)/2#. As area of complete triangle is #1/2axxb#, we have
#r/2(a+b+c)=(ab)/2# and as area of triangle is #12#, we have #a+b+c=24/r# or #r=24/(a+b+c)#.
Here we have two angles #pi/2# and #pi/12# and third angle is #pi-pi/2-pi/12=(5pi)/12# and using sine law, we have
#a/sin(pi/12)=b/sin((5pi)/12)# or #a/b=sin(pi/12)/sin((5pi)/12)#
i.e. #a/b=0.25882/0.96593=0.26795# and as #ab=24#
Hence #b^2=(ab)xxa/b=24xx0.26795#
and #b=sqrt6.4308=2.536# and #a=24/2.536=9.464#
and #c=sqrt(2.536^2+9.464^2)=sqrt95.9986=9.8#
Hence #r=24/(2.536+9.464+9.8)=24/21.8=1.101#
and area of incircle is #pi(1.101)^2=3.808#

