A wrench with a length of #35 cm# is being used to unscrew a #7/2 cm# bolt. If a torque of #36 Nm# is needed to overcome the friction keeping the bolt in place, what is the minimum torque that must be applied to the wrench to unscrew the bolt?
1 Answer
A torque of
Explanation:
This question attempts to trick us with extra information, in this case the distances at which forces are acting. The answer comes from the fact that torque is independent of the distance from the pivot point at which the force is applied. This is because torque is defined as the force multiplied by the distance at which it is applied (details here) :
when the force is applied perpendicular to the axis of rotation as it is in our situation,
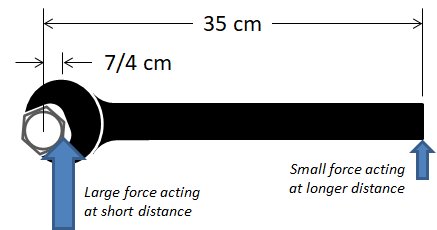
So the torque applied to the wrench is the same as as the torque applied to the bolt even though the force on the wrench is much smaller than the force on the bolt. This is the whole purpose of the wrench, to use the mechanical advantage of distance! Therefore, a torque of

