A yo-yo is made of 3 disks (same material) and the inner one is 3times smaller than the two outer ones (R/r=3). A string (small thickness) is wrapped around the center disk. What will its acceleration be equal to?
2 Answers
Explanation:
Let the mass of the center disk be
The yo-yo would experience a downward gravitational pull of magnitude
Let
# G - T= Sigma F = 19 color(white)(l) m * a#
The three disk revolves around the center of the yo-yo. The equation
#I = 1/2 * m* r^2#
gives the moment of inertia for each of the disk. The yo-yo would, therefore, have a moment of inertia of
#Sigma I = 2 xx 1/2 * 9 color(white)(l) m * (3 color(white)(l) r)^2 + 1/2 * m * r^2 = 163/2 color(white)(l) m * r^2#
The tension force the string exerts on the yo-yo is applied at a distance
#tau = T * r#
The string would drive the yo-yo to spin at an angular acceleration
#alpha = tau / (Sigma I) = (T * r)/(163//2 * m * r^2)#
The equation
#a = alpha * r#
#color(white)(a) = r * tau / (Sigma I) #
#color(white)(a) = r * (T * r)/(163//2 * m * r^2)#
#color(white)(a) = (T)/(163//2 * m )#
Therefore
#T = 163/2 * m * a#
Substituting
#19 color(white)(l) m * g - 163/2 * m * a = 19 color(white)(l) m * a#
#a = 38/201 color(white)(l) g#
Does this result make sense? For reference, a yo-yo consisting of a single disk would experience a liner acceleration equal to
Reference
[1] "Physics of a Yo-Yo", CK-12 Foundation, https://www.ck12.org/physics/physics-of-a-yo-yo/lesson/Yo-Yo-Type-Problems-PPC/
Based on earlier answer by @jacob-t-3
Explanation:
Let the mass of the central disk be
Given is radius of outer disks
The disks are made of same material. It is assumed that thickness of all three is same. Consequently, mass of each outer disk is proportional to its
#=># Mass of each outer disk#=9\ m#
Total weight of yo-yo#M=(2xx9+1)\ m=19\ m#
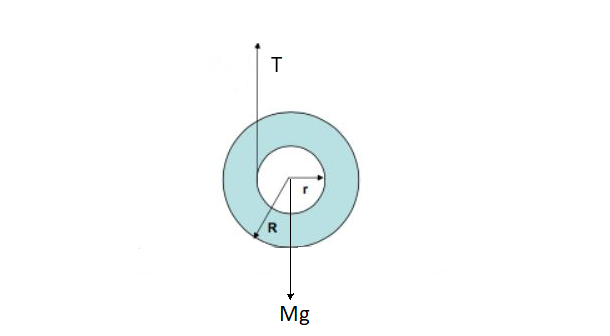
Total weight of yo-yo acts downwards
#:.# Downwards force acting on yo-yo#=19mg# .......(1)
where#g# is acceleration due to gravity.
Let
#F_"net"=Mg-T#
If
#Mg-T=Ma# ......(2)
The three disks revolve around the center of the yo-yo. The moment of inertia of a disk rotating about its center of mass is given as
#I = 1/2 "mass"* "radius"^2#
Total moment of inertia of yo-yo is sum of moments inertia of three disks.
#Sigma I = 2 (1/2 * 9 m * (3 r)^2) + 1/2 m * r^2 #
#=>Sigma I = 162/2\ mcdot r^2 + 1/2 * m * r^2#
#=>Sigma I = 163/2 \ m * r^2#
Weight, which is acting at the center of mass, donot produce any torque. Therefore, total torque
#tau = T * r#
Let this torque produce an angular acceleration
#:.alpha = tau / (Sigma I) = (T * r)/(163/2\ m * r^2)# ....(3)
Expression relating the angular acceleration
#a = r*alpha #
Using (3) we get
#a = r * (T * r)/(163/2 * m * r^2)#
#=>T = 163/2 * m * a#
Substituting
#19\ m * g - 163/2 \ m * a = 19\ m * a#
#=>19\ m * g= 163/2 \ m * a + 19\ m * a#
#=>19\ m * g= 201/2 \ m * a#
#=>a = 38/201\ g#

