Question

ABC is a equilateral triangle. If `|BD|=|CF|` and `|CE|=6`, how do you find `|AD|=x`?

ABC is a equilateral triangle. If `|BD|=|CF|` and `|CE|=6`, how do you find `|AD|=x`?

Answer 1

`AD=x=12` units

Explanation:

Draw a line `DG`, parallel to `AC`, as shown in the figure.
`=> DeltaDBG` is an equilateral triangle.
Let `DB=y, => DG=BG=DB=y`,
Let `angleDEG=w, => angleFEC=w`,
`angleEGD=180-60=120^@`
`angleECF=180-60=120^@`
As `angleEGD=angleECF, angleDEG=angleFEC, and CF=DG`,
`=> DeltaEGD and DeltaECF` are congruent.
`=> EG=EC=6`

Given that `DeltaABC` is an equilateral triangle,
`=> AB=BC`,
`=> AD+DB=BG+GE+EC`,
`=> x+y=y+6+6`,
`=> x=12`

Hence, `AD=x=12` units

Sol. 2)

Draw a line `DH`, parallel to `BC`, as shown in the figure,
`=> DeltaADH` is an equilateral triangle,
`=> DH=AD=x`,
`=> HC=DB=y`,
`=> DeltaDHF and DeltaECF` are similar
`=> (DH)/(HF)=(EC)/(CF)`
`=> x/(2y)=6/y`,
`=> x=12` units

Answer 2

`x=12.`

Explanation:

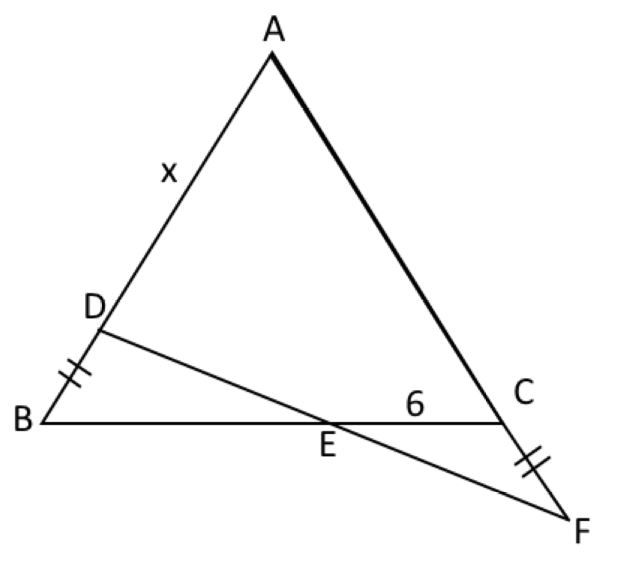
Let us solve the Problem with the help of Trigonometry.

We want to apply the Sine-Rule to `DeltaDBE, and DeltaCEF.`

Hence, we need to find, from `DeltaDBE,`

`"sides "DB, BE, /_DEB, and, /_BDE.`

Similarly, in `DeltaCEF,` we will require,

`"side "CF, "/_EFC, and, /_CEF.`

Suppose that, `BC=a, and, /_EFC=theta.`

`DeltaABC` is equilateral.

`:. AB=BC=CA=a, and, /_B=60, /_ECF=120.`

In `DeltaCEF, /_EFC+/_ECF+ /_CEF=180.`

`:. theta+120+/_CEF=180 rArr /_CEF=60-theta=/_DEB.`

Also, `BD=AB-AD=a-x, &, as CF=BD=a-x.`

Similarly, `BE=BC-EC=a-6.`

In`DeltaCEF, EC=6, CF=a-x, /_EFC=theta, /_CEF=60-theta.`

`:. (CE)/(sin/_EFC)=(CF)/(sin/_CEF).......[because," the sine-rule]."`

`rArr 6/sintheta=(a-x)/sin(60-theta)....................(1).`

Next, in `DeltaDBC, DB=a-x, BE=a-6, /_DEB=60-theta, &`

`/_BDE=180-(/_DBE+/_DEB)=180-(60+60-theta)=60+theta.`

`:.," by the sine-rule, "(DB)/(sin/_DEB)=(BE)/(sin/_BDE).`

`rArr (a-x)/sin(60-theta)=(a-6)/sin(60+theta)..............(2).`

`(1), &, (2) rArr 6/sintheta=(a-6)/sin(60+theta), or,`

`sin(60+theta)/sintheta=(a-6)/6.`

`:. (sin60costheta+cos60sintheta)/sintheta=a/6-6/6.`

`:.sqrt3/2*costheta/sintheta+1/2*sintheta/sintheta=a/6-1.`

`:. sqrt3/2*cottheta+1/2+1=a/6, or, a=3sqrt3cottheta+9....(3).`

Now, from `(1), 6/sintheta=(a-x)/sin(60-theta).`

`:. sin(60-theta)/sintheta=(a-x)/6.`

`:. (sin60costheta-cos60sintheta)/sintheta=(a-x)/6.`

`:. sqrt3/2*costheta/sintheta-1/2*sintheta/sintheta=(a-x)/6.`

`:. 6(sqrt3/2*cottheta-1/2)=(a-x).`

`:. 3sqrt3cottheta-3-a=-x.`

Finally, by `(3),` then,

`x=a+3-3sqrt3cottheta=(3sqrt3cottheta+9)+3-3sqrt3cottheta.`

`rArr x=12,` as Respected CW has already obtained!

Enjoy Maths.!