Question

Acceleration is related to distance and time by the following expression: `a = 2xt^p`. Find the power `p` that makes this equation dimensionally consistent?

Answer 1

`p=-2`

Explanation:

All you have to do here is replace the quantities given to you in that equation with their corresponding dimensions, which as you know are

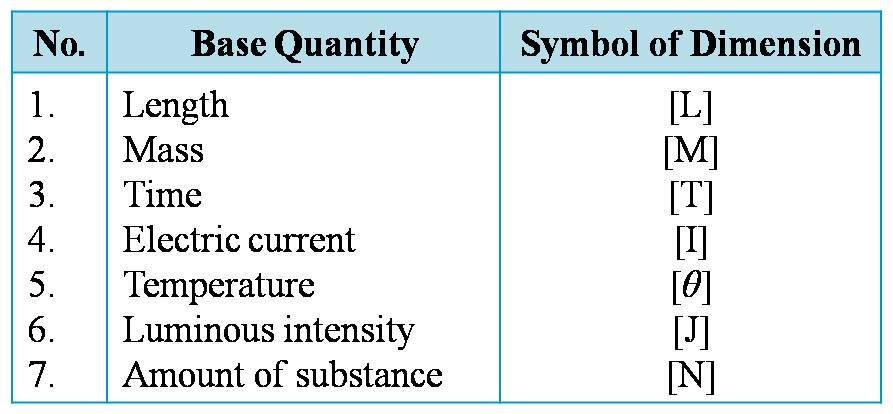https://physicsforus.wordpress.com/physics-1/magnitude-and-units/c-dimensi/

So, you know that you have

• `"distance" = x -> ["L"]`
• `"time" = t -> ["T"]`

Now, your equation looks like this

`a = 2 * x * t^p`

Since you must match dimensions here, you can eliminate the `2`, a dimensionless quantity, altogether to get

`a = x * t^p`

As you know, acceleration, `a`, tells you the rate at which the velocity of an object, `v`, changes with respect to time, `t`.

Velocity, on the other hand, tells you the rate at which the position of an object, `x`, changes with respect to a given frame of reference, and also with respect to time.

So, if position, or distance, has the dimension of `["L"]` and time has the dimension of `["T"]`, you can say that velocity will have the dimensions of

`v = ["L"] * ["T"]^(-1) ->` distance over time

Consequently, acceleration will have dimensions of

`a = ["L"] * ["T"]^(-1) * ["T"]^(-1)`

`a = ["L"] * ["T"]^(-2) ->` veloctiy over time

This means that the left side of the equation is

`["L"] * ["T"]^(-2) = x * t^p`

On the right side of the equation, replace `x` and `t` with their respective dimensions to get

`["L"] * ["T"]^(-2) = ["L"] * ["T"]^p`

At this point, it becomes clear that `p=-2`, since

`color(red)(cancel(color(black)(["L"]))) * ["T"]^(-2) = color(red)(cancel(color(black)(["L"]))) * ["T"]^p`

`["T"]^(-2) = ["T"]^p implies color(green)(bar(ul(|color(white)(a/a)color(black)(p = -2)color(white)(a/a)|)))`