After 42 days a 2.0 g sample of phosphorus-32 contains only 0.25 g of the isotope. What is the half-life of phosphorus-32?
2 Answers
May 13, 2018
14 days
Explanation:
Mass of atoms initially,
Mass after 42 days,
we have,
if half life is
then
or
May 13, 2018
The half life is
Explanation:
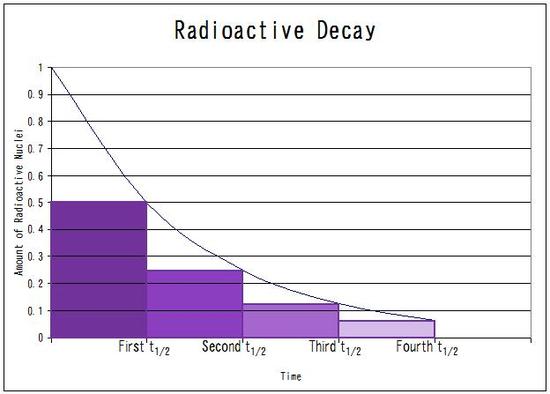
The proportion of
This represents
Therefore,
The half life is


