Question

An angle Ɵ in standard position for which terminal side passes through the point (-3,1/2), how do you find the six trig functions for Ɵ?

Answer 1

See below.

Explanation:

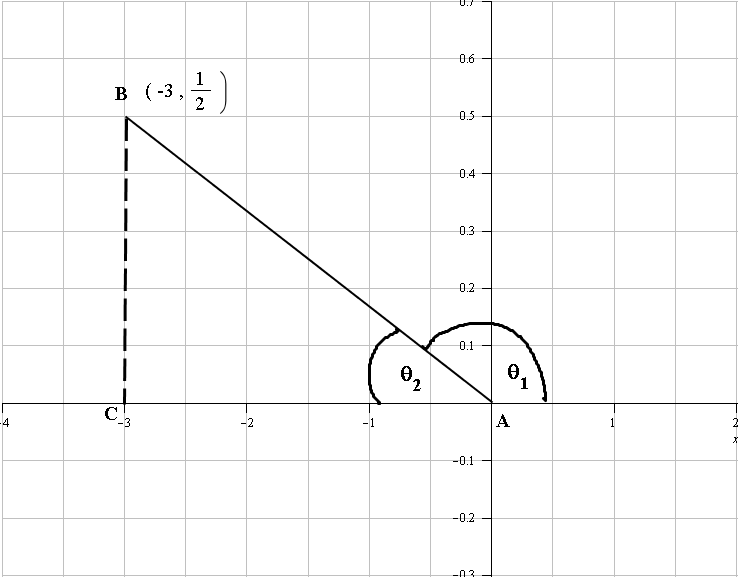
We measure the trigonometric ratios from the triangle that is formed in the quadrant in which the terminal side finishes. From the diagram we can see that the terminal side is in the II quadrant. We therefore use the triangle ABC

`bb(AC)=-3`

`bb(BC)=1/2`

By Pythagoras' theorem:

`bb((AB)^2)=bb((BC)^2)+bb((AC)^2)`

`bb(AB)=sqrt(bb((BC)^2)+bb((AC)^2)`

`bb(AB)=sqrt((1/2)^2+(-3)^2)=sqrt(37/4)=sqrt(37)/37`

`sintheta_2=(bb(BC))/(bb(AB))=(1/2)/(sqrt(37)/37)=(37 /2)/sqrt(37)=color(blue)(sqrt(37)/2)`

`costheta_2=(bb(AC))/(bb(AB))=(-3)/(sqrt(37)/37)=(-111)/sqrt(37)=(-111sqrt(37))/37=color(blue)(-3sqrt(37))`

`tantheta_2=(bb(BC))/(bb(AC))=(1/2)/(-3)=color(blue)(-1/6)`

For the reciprocal ratios we can use:

`csctheta_2=1/sintheta_2=1/(sqrt(37)/2)=2/sqrt(37)=color(blue)((2sqrt(37))/37)`

`sectheta_2=1/costheta_2=1/(-3sqrt(37))=color(blue)(-sqrt(37)/111)`

`cottheta_2=1/tantheta_2=1/(-1/6)=color(blue)(-6)`