An isosceles trapezoid has bases of length 23 and 12 centimeters and legs of length 13 centimeters. What is the area of the trapezoid to the nearest tenth?

Question

6441 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2016-02-07T14:06:39

#205.9sq.cm#

Area of trapezium=#1/2(a+b)h=((a+b)h)/2#

Where #a and b=parall##e##l# #sides,h=height#

Now in an isoceles trapezium the legs are equal ,and in this case they are in a length of #13#

Now consider the diagram:
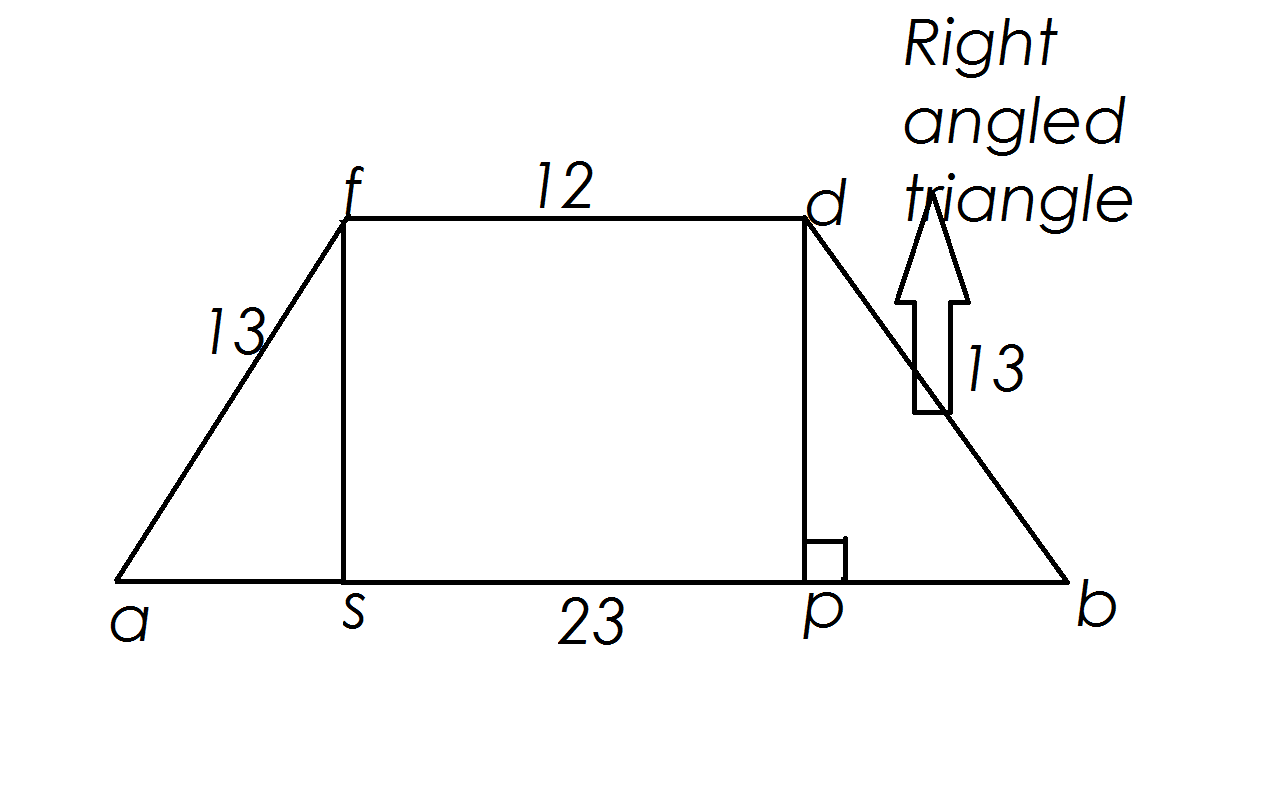
enter image source here

Now we will have a short sypnosis of the lengths:

#ab=23,fd=12,dp=fs=h#

Now we need to find the height:In this case the height is in a right triangle.So,we use the pythagorean theorem:

#a^2+b^2=c^2#

Where #a# and #b# are the two adjacent sides,#c=hypoten##use# (longest side)

But we should know the length of #pb# to know the height:

#rarrpb=(23-12)/2=11/2=5.5#

We divide it by #2# because there is another side as #as# which equals #pb# :

So,

#rarrh^2+5.5^2=13^2#

#rarrh^2+30.25=169#

#rarrh^2=169-30.25#

#rarrh^2=138.75#

#rarrh=sqrt138.25=11.77#

Now,

#Area=((23+12)11.77)/2#

#rarr=((35)11.77)/2#

#rarr=411.9/2=205.95sq.cm^2#

If we round it off to the nearest tenths we get #205.9sq.cm^2#