An isosceles triangle has sides A, B, and C, such that sides A and B have the same length. Side C has a length of #5 # and the triangle has an area of #35 #. What are the lengths of sides A and B?
1 Answer
May 23, 2018
Explanation:
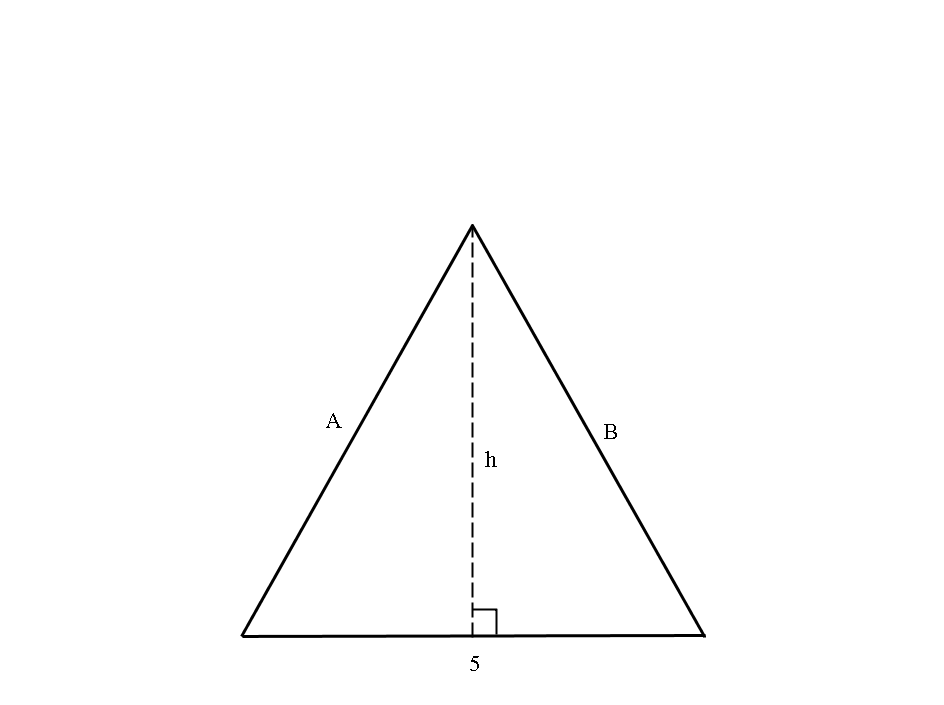
The area of a triangle is given by:
By Pythagoras' theorem:
2 d.p.

