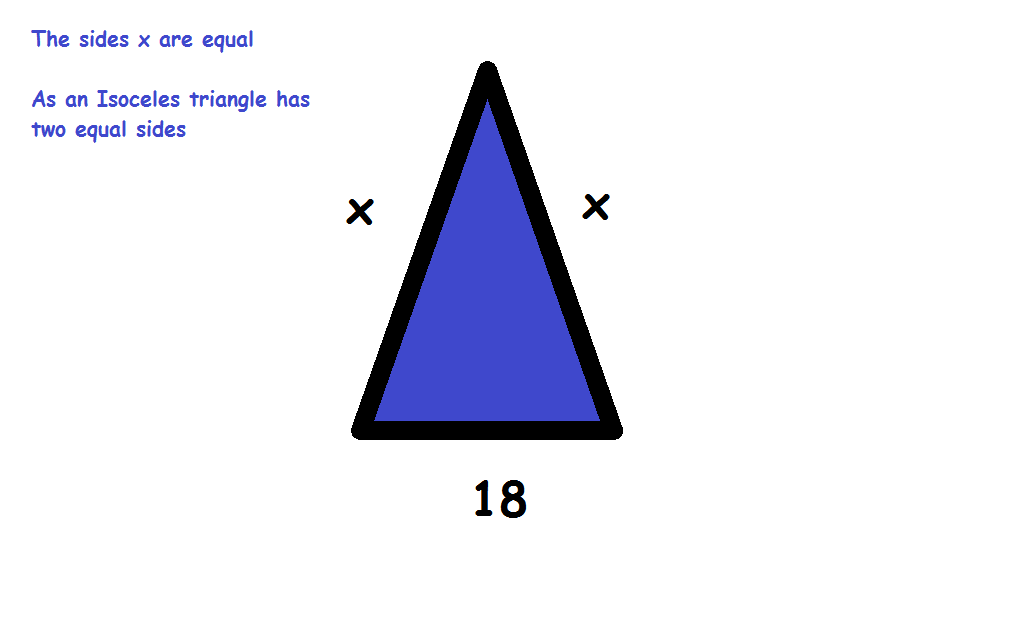
We can use the Heron's formula for area of a Triangle
#color(blue)("Area"=sqrt(s(s-a)(s-b)(s-c))#
Where,
#color(orange)("a, b and c are the sides"#
#color(orange)("s = semi-perimeter"=(a+b+c)/2#
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Let's assign the values
#color(purple)(a=x#
#color(purple)(b=x#
#color(purple)(c=18#
#color(purple)(s=(x+x+18)/2=(2x+18)/2#
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Let's start to solve
The whole equation starts here
#rArrcolor(violet)(sqrt((2x+18)/2((2x+18)/2-x)((2x+18)/2-x)((2x-18)/2-18))=64#
The whole equation equals #64# as, the area is #64#
#rarrsqrt((2x+18)/2((2x+18-2x)/2)((2x+18-2x)/2)((2x+18-36)/2))=64#
#rarrsqrt((2x+18)/2((color(red)(2x)+18-color(red)(2x))/2)((color(red)(2x)+18-color(red)(2x))/2)((2x-18-36)/2))=64#
#rarrsqrt((2x+18)/2((color(red)(2x-2x)+18)/2)((color(red)(2x-2x)+18)/2)((2x-18-36)/2))=64#
#rarrsqrt((2x+18)/2((color(red)(18))/2)((color(red)(18))/2)((2x-18-36)/2))=64#
#rarrsqrt((2x+18)/2(color(red)(9))(color(red)(9))((2x+18-36)/2))=64#
#rarrsqrt((2x+18)/2(color(red)(81))((2x+18-36)/2))=64#
#rarrsqrt((2x+18)/2(81)((2x+color(pink)(18-36))/2))=64#
#rarrsqrt((2x+18)/2(81)((2xcolor(pink)(-18))/2))=64#
Square both sides to take out the radical sign
#rarr(sqrt((2x+18)/2(81)((2x-18)/2)))^2=64^2#
#rarr((2x+18)/2)(81)((2x-18)/2)=color(red)(64*64)#
#rarr((2x+18)/2)(81)((2x-18)/2)=color(red)(4096)#
#rarrcolor(indigo)(((2x+18)/2)((2x-18)/2))(81)=color(red)(4096)#
Take out the common factor #2#
#rarrcolor(indigo)(((2(x+9))/2)((2(x-9))/2))(81)=color(red)(4096)#
#rarrcolor(indigo)(((cancel2(x+9))/cancel2)((cancel2(x-9))/cancel2))(81)=4096#
#rarrcolor(indigo)((x+9)(x-9))(81)=4096#
Use the indentity #color(brown)((a+b)(a-b)=a^2-b^2#
#rarrcolor(indigo)((x^2-9^2))(81)=4096#
#rarr(x^2-81)(81)=4096#
#rarr81x^2-81*81=4096#
#rarr81x^2-6561=4096#
#rarr81x^2=4096+6561#
#rarr81x^2=10657#
#rarrx^2=10567/81#
#rarrx^2=131.56#
Take the square root of both sides
#rarrsqrt(x^2)=sqrt(131.56)#
#color(green)(rArrx=11.47#


