An isosceles triangle has sides A, B, and C, such that sides A and B have the same length. Side C has a length of $4$ $4$ and the triangle has an area of $128$ $128$ . What are the lengths of sides A and B?

Question

An isosceles triangle has sides A, B, and C, such that sides A and B have the same length. Side C has a length of $4$ $4$ and the triangle has an area of $128$ $128$ . What are the lengths of sides A and B?

1 Answer

Impact of this question

1585 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-11-11T20:54:26

$A = B = 10 \sqrt{41}$ $A=B=10sqrt41$

Explanation:

When in doubt, draw a diagram.

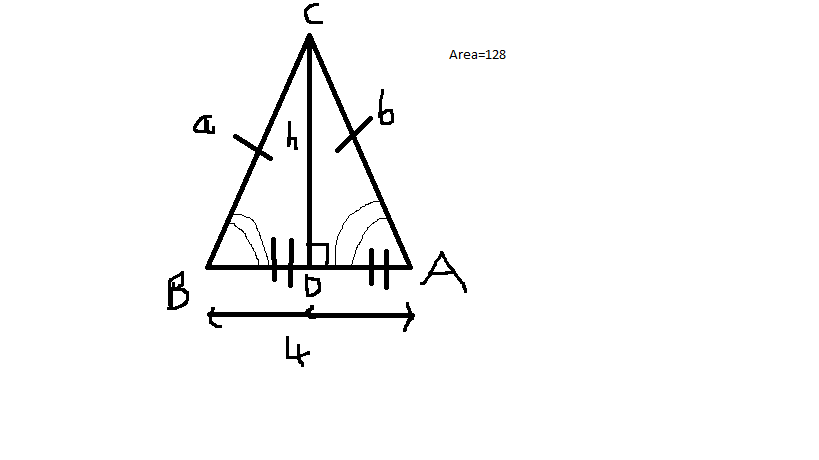
enter image source here
$h$ $h$ is the perpendicular bisector of $A B$ $AB$ from $C$ $C$ , and meets $A B$ $AB$ at point $D$ $D$ .

Sidenote: I have labeled this diagram according to the convention, with angles $A, B$ $A, B$ and $C$ $C$ opposite sides $a, b$ $a, b$ and $c$ $c$ respectively. So where you have $A$ $A$ and $B$ $B$ , I have $a$ $a$ and $b$ $b$ . Just a note.

We know that $A r e a = \frac{1}{2} \times b a s e \times h e i g h t$ $Area=1/2xxbasexxheight$ . In here, the base is length 4, and the height is $h$ $h$ .

$128 = \frac{1}{2} \times 4 h$ $128=1/2xx4h$
$128 = 2 h$ $128=2h$
$h = 64$ $h=64$

Now, focus just on $△ B C D$ $triangleBCD$ (or $△ A C D$ $triangle ACD$ ). To work out the remaining length $a$ $a$ (and $b = a$ $b=a$ since the $△$ $triangle$ is isosceles) we need to use the Pythagorean Theorem. We have a base of 2, since it is half of the length 4 (remember that $h$ $h$ is a bisector).

$2^{2} + 64^{2} = a^{2}$ $2^2+64^2=a^2$
$a^{2} = 4100$ $a^2=4100$
$a = \sqrt{4100} = 10 \sqrt{41}$ $a=sqrt4100=10sqrt41$

Convert back to the format given in the question:

$A = B = 10 \sqrt{41}$ $A=B=10sqrt41$

Science

Math

Humanities

... and beyond

An isosceles triangle has sides A, B, and C, such that sides A and B have the same length. Side C has a length of $4$ $4$ and the triangle has an area of $128$ $128$ . What are the lengths of sides A and B?

1 Answer

Explanation:

Related questions

Impact of this question

Science

Math

Humanities

... and beyond

An isosceles triangle has sides A, B, and C, such that sides A and B have the same length. Side C has a length of 44 and the triangle has an area of 128128 . What are the lengths of sides A and B?

1 Answer

Explanation:

Related questions

Impact of this question

An isosceles triangle has sides A, B, and C, such that sides A and B have the same length. Side C has a length of $4$ $4$ and the triangle has an area of $128$ $128$ . What are the lengths of sides A and B?