An isosceles triangle has sides A, B, and C, such that sides A and B have the same length. Side C has a length of #32 # and the triangle has an area of #16 #. What are the lengths of sides A and B?
1 Answer
Nov 13, 2017
Explanation:
First things first - we start off with a diagram!
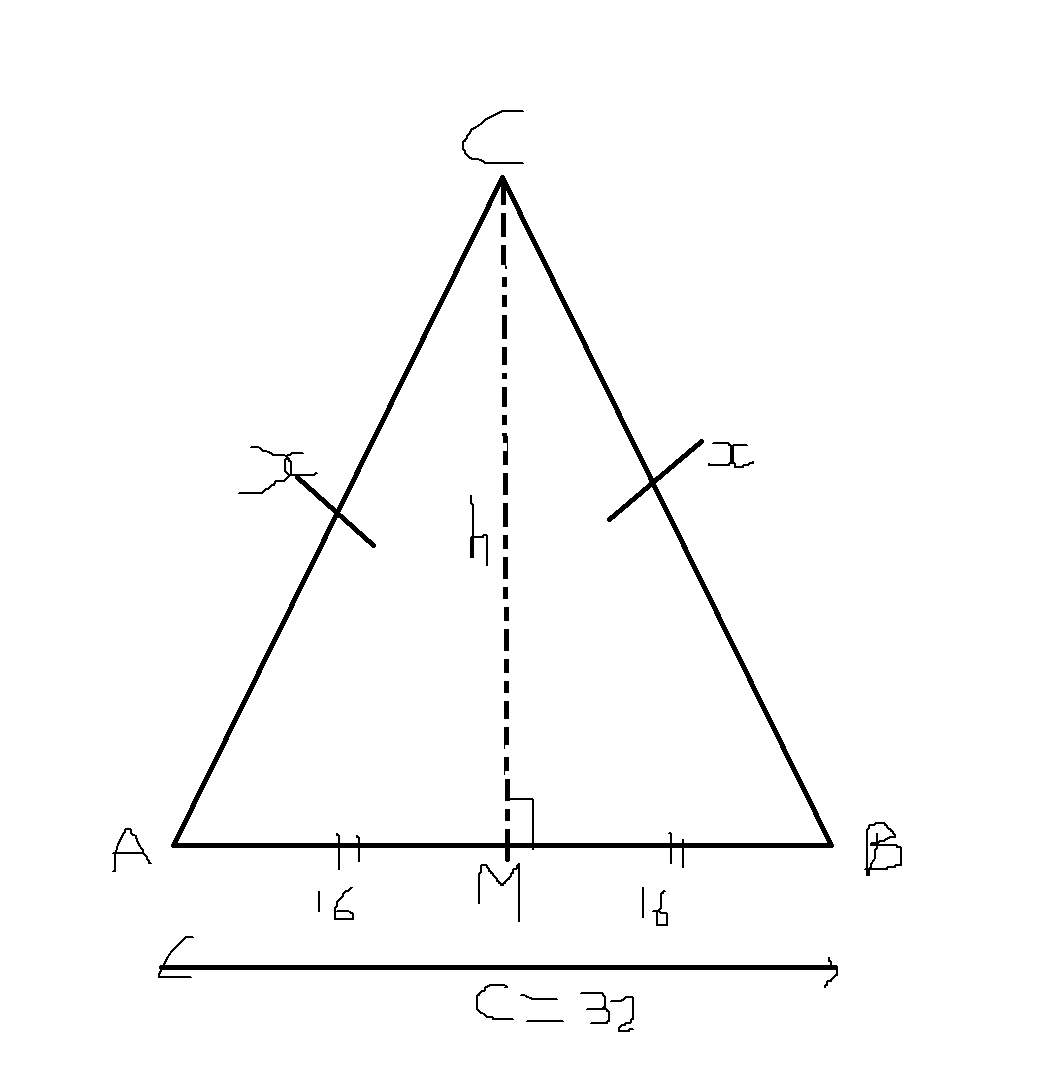
Not the most elegant diagram in the world, but it does the job. By convention, the side opposite angle
Let
Now, we can apply Pythagoras' Theorem in one of the right-angled triangles. We have the height
