Question

An isosceles triangle has sides A, B, and C with sides B and C being equal in length. If side A goes from `(4 ,1 )` to `(8 ,9 )` and the triangle's area is `64`, what are the possible coordinates of the triangle's third corner?

Answer 1

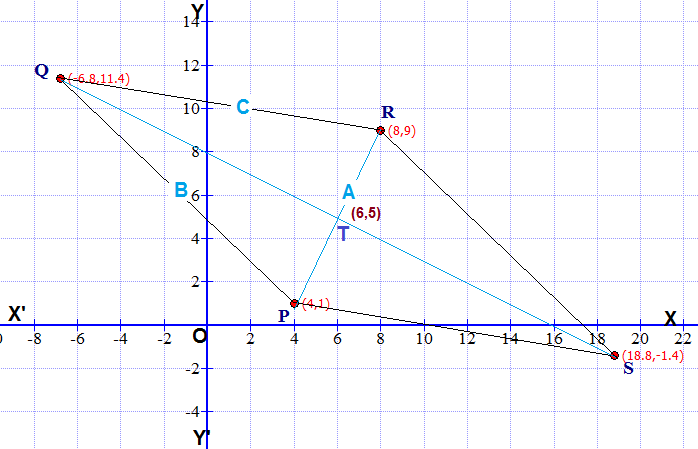
Let `PR=A` be the side of the isosceles triangle having coordinates of its end points as follows

`Pto(4,1)` and `Rto (8,9)`

Let the coordinates of the third point of the triangle be `(x,y)`.

As `(x,y)` is equidistant from P and R we can write

`(x-4)^2+(y-1)^2=(x-8)^2+(y-9)^2`

`=>x^2-8x+16+y^2-2y+1=x^2-16x+64+y^2-18y+81`

`=>8x+16y=128`

`=>x+2y=16`

`=>x=16-2y......[1]`

Again `(x,y)` being equidistant from P and R, the perpendicular dropped from `(x,y)` to `PR` must bisect it, Let this foot of the perpendicular or mid point of `PR` be `T`

So coordinates of `Tto(6,5)`

Now height of the isosceles triangle

`H=sqrt((x-6)^2+(y-5)^2)`

And the base of the isosceles triangle

`PR=A=sqrt((4-8)^2+(1-9)^2)=4sqrt5`

So by the problem its area

`1/2xxAxxH=64`

`=>H=128/A=128/(4sqrt5)=32/sqrt5`

`sqrt((x-6)^2+(y-5)^2)=32/sqrt5`

`=>(x-6)^2+(y-5)^2=1024/5=204.8....[2]`

By [2] and [1] we get

`(16-2y-6)^2+(y-5)^2=204.8`

`=>(10-2y)^2+(y-5)^2=204.8`

`=>5y^2-50y+125==204.8`

`=>y^2-10y+25==40.96`

`=>(y-5)^2=6.4^2`

`=>y=5pm6.4`

So `y=11.4 and y= -1.4`

when `y=11.4`

`x=16-2xx11.4=-6.8`

when `y=-1.4`

`x=16-2xx(-1.4)=18.8`

So the coordinates of third point will be

`(-6.8,11.4)to"Q in figure"`

OR

`(18.8,-1.4)to"S in figure"`