An isosceles triangle has sides A, B, and C with sides B and C being equal in length. If side A goes from #(7 ,1 )# to #(8 ,5 )# and the triangle's area is #32 #, what are the possible coordinates of the triangle's third corner?
2 Answers
The possible points are
Explanation:
Given:
The endpoints of side A are
Let side
Find the length of the base:
The area of a triangle is:
Substitute in the values of Area and Base:
Compute midpoint of side A
Find the two points that are the same distance as height away from the midpoint:
We need the slope of side A:
The slope of the height is perpendicular to side A:
Use the point slope form of the equation of a line to write the equation for the height:
With equations [1] and [2] this ugly, I am going to use WolframAlpha to solve them:
The possible points are
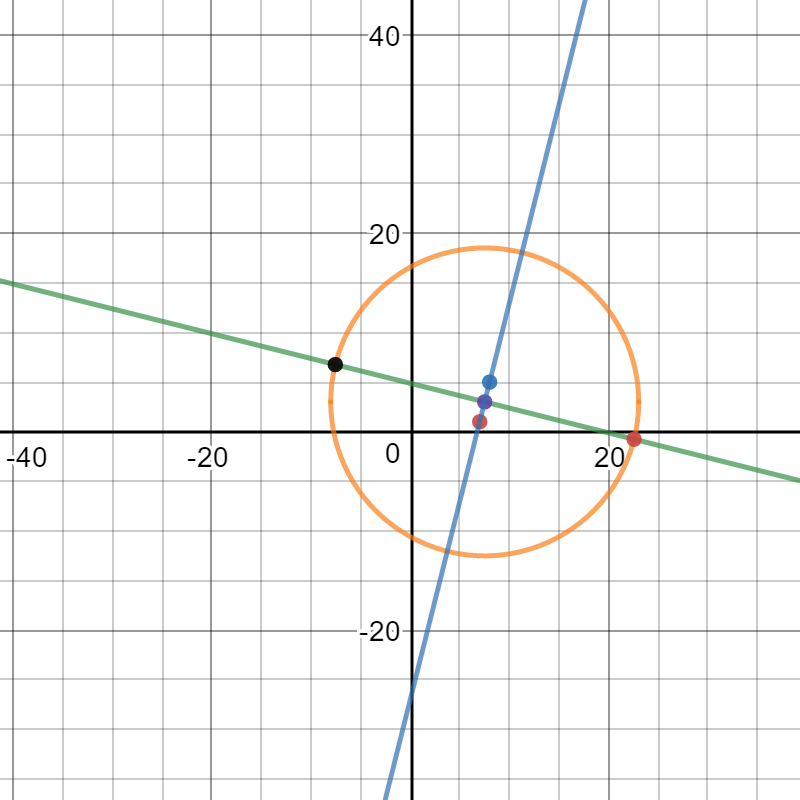
Here is an image of all of the parts of this problem that should show you that the answer is correct:
Explanation:
We solve this Problem deploying the methods of Analytic Geometry.
Supoose that the third vertex of the triangle is
Recall that, the Area of a Triangle having vertices
Hence, in our case, since the area is
Also, Length of side B = Length of side C
Solving
Thus, the possible third vertex can be
Enjoy Maths.!
