An isosceles triangle has sides A, B, and C with sides B and C being equal in length. If side A goes from #(1 ,4 )# to #(5 ,1 )# and the triangle's area is #15 #, what are the possible coordinates of the triangle's third corner?
2 Answers
The two vertices form a base of length 5, so the altitude must be 6 to get area 15. The foot is the midpoint of the points, and six units in either perpendicular direction gives
Explanation:
Pro tip: Try to stick to the convention of small letters for triangle sides and capitals for triangle vertices.
We're given two points and an area of an isosceles triangle. The two points make the base,
The foot
The direction vector from between the points is
Since the area
So we need to move
Check:
The signed area is then half the cross product
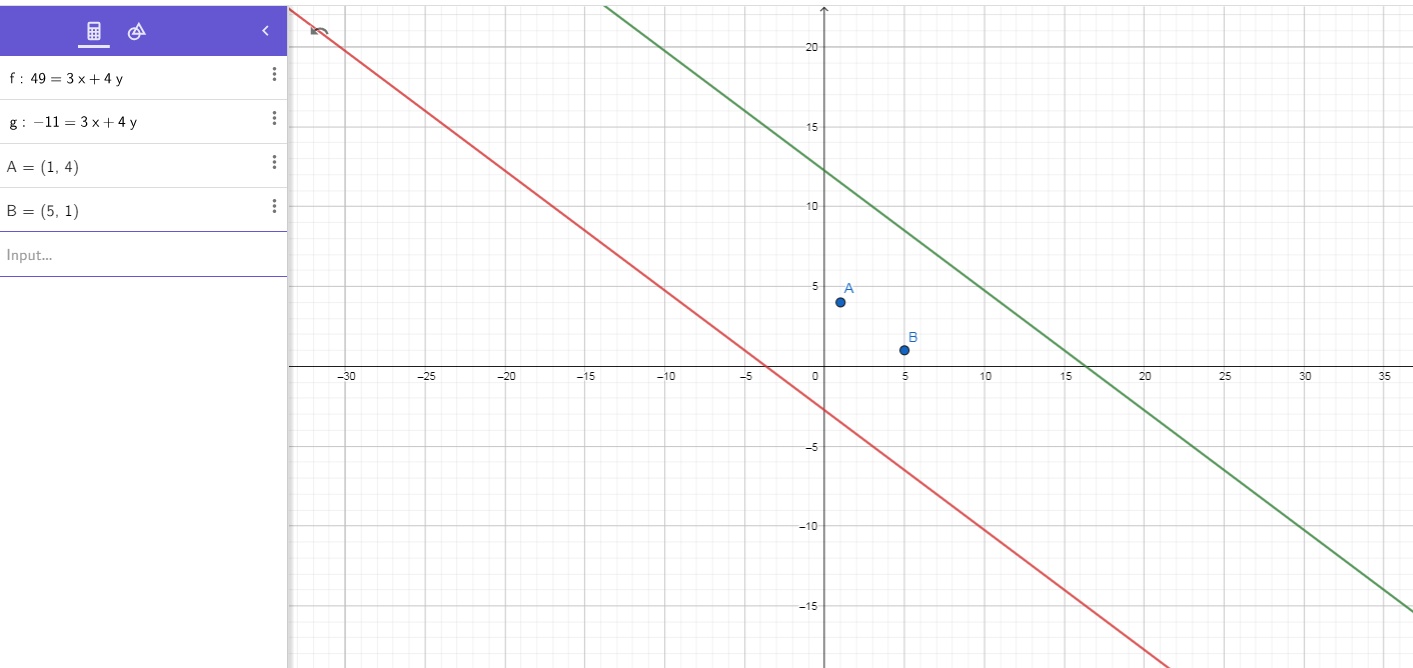
That's the end, but let's generalize the answer a bit. Let's forget about it being isosceles. If we have C(x,y), the area is given by the shoelace formula:
The area is
So if the vertex C is on either of those two parallel lines, we'll have a triangle of area 15.
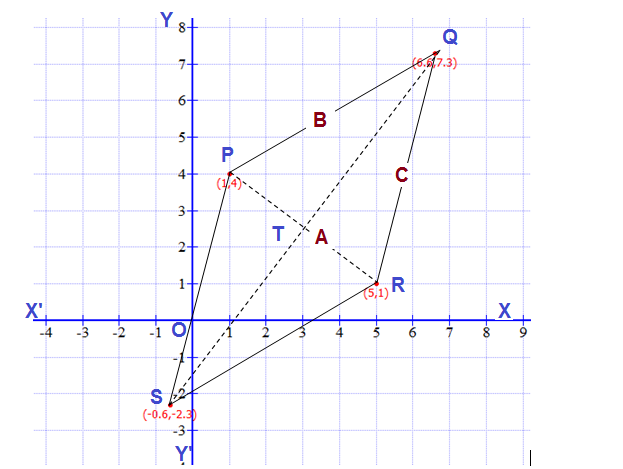 Let
Let
Let the coordinates of the third point of the triangle be
As
Again
So coordinates of
Now height of the isosceles triangle
And the base of the isosceles triangle
So by the problem its area
By [2] and [1] we get
So
when
when
So the coordinates of third point will be
OR


