#"Initial KE"=(E_i)=32kJ=32xx10^3J#
After 4s
#"Final KE"=(E_f)=72kJ=72xx10^3J#
KE uniformly increases, so it will have a constant positive slope when plotted against time and this slope will be #(Delta E)/(Deltat)=(E_f- E_i)/(Delta t)=((72-32)xx10^3)/4=10^4J/s#
#,"where "Delta t=4s#
If at t th instant (# t in [0,4]#) the velocity of the mass be #v# then the KE at #t# th instant
#E_t=1/2xxmxxv^2=1/2xx2xxv^2=v^2#
#",where mass "m= 2kg#
Now #(E_t-E_i)/(t-0)=(v^2-32xx10^3)/(t-0)=10^4#
#=>v^2=10^4xxt+32xx10^3#
#=>v=sqrt(10^4xxt+32xx10^3)#
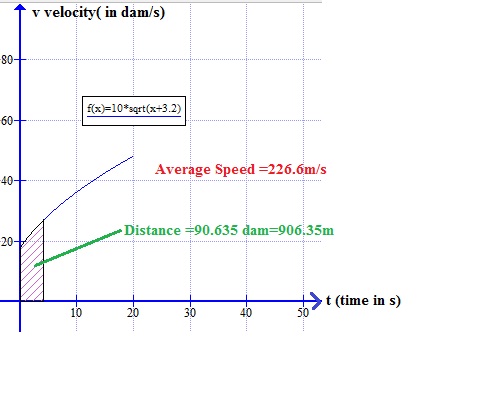
#=sqrt(10^4(t+3.2))#
#=10^2sqrt(t+3.2)#
Now distance traversed during 4 s
#S=int_0 ^4vdt=int_0 ^4 10^2(sqrt(t+3.2))dt#
Let #z^2=t+3.2#
#2zdz=dt#
when # t=0;# then #z =sqrt3.2 #
when # t=4;# then #z =sqrt7.2 #
#S=int_0 ^4vdt=int_0 ^4 10^2(sqrt(t+3.2))dt#
#S =int_(sqrt(3.2))^(sqrt7.2) 10^2xx2z^2dz#
# =int_(sqrt(3.2)) ^(sqrt7.2) 200xxz^2dz#
#=200/3xx[(sqrt7.2)^3-(sqrt3.2)^3]m#
Hence the average speed #="distance" /"time"=S/4#
#=200/3xx[(sqrt7.2)^3-(sqrt3.2)^3]/4=226.6m/s#