An object's two dimensional velocity is given by #v(t) = ( tsin(pi/3t) , 2cos(pi/2t )- t )#. What is the object's rate and direction of acceleration at #t=2 #?

Question

1520 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2016-04-18T08:31:31

#color(red)(a_x(2)=-0,184)#
#color(green)(a_y(2)=-1)#
#a(2)=1,017 #

enter image source here

#v(t)=(t sin(pi/3t) ,2 cos(pi/2t)-t)#

#a_x(t)=d/(d t)(t sin(pi/3t))=1*sin(pi/3t)+t*pi/3cos(pi/3t) #

#a_x(2)=sin(2pi/3)+2*pi/3*cos(2pi/3)#

#a_x(2)=0,866+2*pi/3*(-1/2)#

#a_x(2)=0,866-pi/3#

#a_x(2)=0,866-1,05#

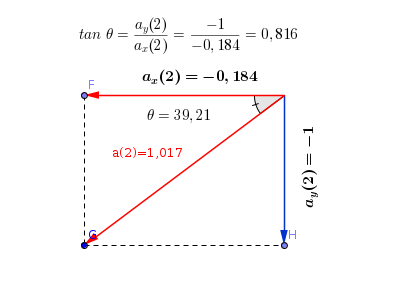
#color(red)(a_x(2)=-0,184)#

#a_y(t)=d/(d t)(2 cos(pi/2t)-t)#

#a_y(t)=-2*pi/2*sin(pi/2t)-1#

#a_y(t)=-pi*sin(pi/2t)-1#

#a_y(2)=-pi*sin(pi/2*2)-1#

#a_y(2)=-pi*sinpi-1" "sin pi=0#

#a_y(2)=-pi*0-1#

#color(green)(a_y(2)=-1)#

#a(2)=sqrt((a_x(2))^2+((a_y(2))^2))#

#a(2)=sqrt((-0,184)^2+(-1)^2))#

#a(2)=sqrt(0,034+1)#

#a(2)=sqrt(1,034)#

#a(2)=1,017 #