Question

An object's velocity is given by `v(t) = (t^2 +t +1 , t^3- 3t )`. What is the object's rate and direction of acceleration at `t=6`?

Answer 1

`vecv(t)=(t^2+t+1)hati+(t^3-3t)hatj`
Differentiating w.r.t. twe have acceleration
`veca(t)=d/(dt)(v(t))=(2t+1)hati+(3t^2-3)hatj`
Acceleration at t=6 is
`veca(6)=(2xx6+1)hati+(3xx6^2-3)hatj=13hati+105hatj`
Magnitude of acceleration
`|veca(6)|=sqrt(13^2+105^2)=105.8`
Direction =`tan^-1(105/13)~~83^o` with the x-axis

Answer 2

`a=105,80 " "(unit)/s^2`

Explanation:

`a(t)=d/(d t) v(t)" derivative of v(t) give us a(t)"`

`"derivative of v(t) for x direction:"`
`"..................................................."`
`a_x(t)=d/(d t)(t^2+t+1)`

`a_x(t)=2t+1`

`"fill in t=6"`

`a_x(6)=2*6+1=13`

`a_x(6)=13`

`"derivative of v(t) for y direction"`
`"..................................................."`
`a_y(t)=d/(d t)(t^3-3t)`

`a_y(t)=3t^2-3`

`"fill in t=6"`

`a_y(6)=3*6^2-3=3*36-3=108-3=105`

`"acceleration is a vector quantity so that we have to add " a_x and a_y " as vector"`

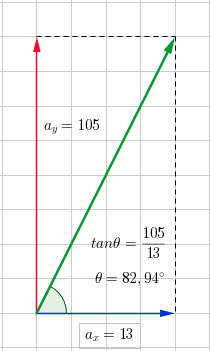
`a=sqrt(13^2+105^2)`

`a=sqrt(169+11025)`

`a=sqrt(11194)`

`a=105,80 " "(unit)/s^2`