Question

Another Thermo Question?

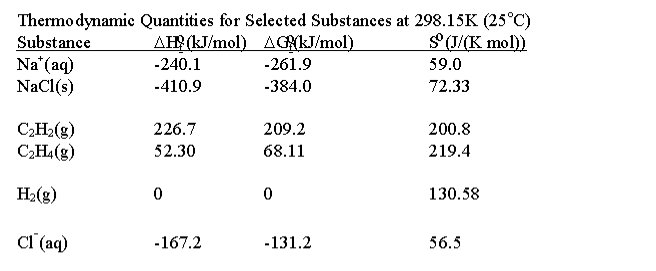
Consider the reaction
C2H2(g) + H2(g) <->C2H4(g). Use the data in
the table above for the following:

A: Estimate Delta G, H and S for the reaction above at 25C, and
use your results to show that the reaction is spontaneous at room
temperature.

B: As the temperature increases, the reaction ceases to be
spontaneous. Use the Gibbs-Helmholtz equation to predict the
temperature at which the reaction is no longer spontaneous for 1 atm
pressure in each gas.

Answer 1

PART A

Part A is fairly straightforward, and is just asking you to choose the thermodynamic values to use. Let `Y` be a thermodynamic state function. Then:

If `G` or `H`:

`DeltaY_"rxn"^@ = sum_P nu_P DeltaY_(f,P)^@ - sum_R nu_R DeltaY_(f,R)^@`

If `S`:

`DeltaS_"rxn"^@ = sum_P nu_P S_(P)^@ - sum_R nu_R S_(R)^@`

where:

• `DeltaY_f^@` is some thermodynamic function of formation (such as Gibbs energy of formation or enthalpy of formation) for one pure substance.
• `S^@` is the standard molar entropy for one pure substance, and `P` (or `R`) stands for products (or reactants). This is defined a little differently because the initial state is at `"0 K"`, and `S_("0 K") = 0` from the third law of thermodynamics.
• `nu` is the stoichiometric coefficient of the substance in the balanced chemical reaction.

`"C"_2"H"_2(g) + "H"_2(g) rightleftharpoons "C"_2"H"_4(g)`

We'll choose `G` first (at `"298.15 K"` and `"1 atm"` like usual):

`color(blue)(DeltaG_"rxn"^@) = nu_(C_2H_4(g))DeltaG_(f,C_2H_4(g))^@ - [nu_(C_2H_2(g))DeltaG_(f,C_2H_2(g))^@ + nu_(H_2(g))DeltaG_(f,H_2(g))^@]`

`= (1)("68.11 kJ/mol") - [(1)("209.2 kJ/mol") +(1) ("0 kJ/mol")]`

`= color(blue)(-"141.1 kJ/mol")`

Already we can say that the reaction is spontaneous at room temperature, since `bb(DeltaG < 0)`, which by definition says the reaction is spontaneous, and standard thermodynamic temperature (`"298.15 K"`, or `25^@ "C"`) is room temperature.

Essentially the same math follows for `DeltaH_"rxn"^@`:

`color(blue)(DeltaH_"rxn"^@) = nu_(C_2H_4(g))DeltaH_(f,C_2H_4(g))^@ - [nu_(C_2H_2(g))DeltaH_(f,C_2H_2(g))^@ + nu_(H_2(g))DeltaH_(f,H_2(g))^@]`

`= (1)("52.30 kJ/mol") - [(1)("226.7 kJ/mol") +(1) ("0 kJ/mol")]`

`= color(blue)(-"174.4 kJ/mol")`

which says the reaction is exothermic, i.e. it releases energy into the surroundings.

And for `DeltaS_"rxn"^@`, you have two options. Either follow the same math as above again, which gives you `-"111.98 J/mol"cdot"K"`, or use:

`DeltaG_"rxn"^@ = DeltaH_"rxn"^@ - TDeltaS_"rxn"^@`

and solve for `DeltaS_"rxn"^@` to get:

`color(blue)(DeltaS_"rxn"^@) = (DeltaH_"rxn"^@ - DeltaG_"rxn"^@)/T`

`= color(blue)(-"111.69 J/mol"cdot"K")`
(don't forget to convert from `"kJ"` to `"J"`).

which means the entropy of the system decreases, meaning that the entropy of the surroundings increases.

Either way, there's about a `0.26%` (i.e. negligible) difference between the two methods, so either way works fine when determining `DeltaS_"rxn"^@`.

PART B

I'm surprised you are asked to use the Gibbs-Helmholtz equation... Because this is what I see on Wikipedia:

`((del(DeltaG_("rxn")^@"/"T))/(delT))_P = -(DeltaH_("rxn")^@)/T^2`

If we want the reaction to no longer be spontaneous, then we must have that `DeltaG_"rxn"^@` at some new temperature `T_"nonspont."` be equal to `0`. There's an easy and a hard way to do this...

The easy way

`cancel(DeltaG_"rxn"^@)^"assumed 0" = DeltaH_"rxn" - T_"nonspont."DeltaS_"rxn"^@`

`=> DeltaH_"rxn"^@ = T_"nonspont."DeltaS_"rxn"^@`

`color(blue)(T_"nonspont.") = (DeltaH_"rxn"^@)/(DeltaS_"rxn"^@)`

`= (-"174.4 kJ/mol")/(-"0.11169 kJ/mol")`

`=` `color(blue)("1561.5 K")`

The hard way

From `((del(DeltaG_("rxn")^@"/"T))/(delT))_P = -(DeltaH_("rxn")^@)/T^2`:

Let us multiply both sides by `dT` at constant pressure. Then:

`d(DeltaG_"rxn"^@"/"T) = -(DeltaH_"rxn"^@)/T^2dT`

Integrating both sides from the initial temperature `T^@` to the final temperature `T_"nonspont."`, we get:

`int_(T^@)^(T_"nonspont.") d(DeltaG_"rxn"^@"/"T') = DeltaH_"rxn"^@int_(T^@)^(T_"nonspont.")-1/(T')^2dT'`

where we have assumed that `DeltaH_"rxn"^@` does not change significantly at a new temperature, but we haven't assumed that for `DeltaG_"rxn"^@`. We have also substituted `T' = T` to not confuse the `T` in the `1/T` with the `T` in the integral bounds.

The integral of a derivative cancels out on the left side, and the right side integrates to give `1/T`, so:

`|[(DeltaG_"rxn"^@(T'))/(T')]|_(T^@)^(T_"nonspont.") = DeltaH_"rxn"^@|[(1/(T'))]|_(T^@)^(T_"nonspont.")`

`(DeltaG_"rxn"^@(T_"nonspont."))/T_"nonspont." - (DeltaG_"rxn"^@(T^@))/T^@ = DeltaH_"rxn"^@[1/(T_"nonspont.") - 1/T^@]`

Now, if we set `T^@ = "298.15 K"` and `T_"nonspont."` to be our new temperature at which `DeltaG_"rxn"^@(T_"nonspont.") = 0`, then:

`cancel((DeltaG_"rxn"^@(T_"nonspont."))/T_"nonspont.")^(0) - (stackrel("Known")overbrace(DeltaG_"rxn"^@(T^@)))/T^@ = stackrel("Known")overbrace(DeltaH_"rxn"^@)[1/T_"nonspont." - 1/T^@]`

Now we'd solve for `T_"nonspont."` to find the temperature at which the reaction is no longer spontaneous (i.e. has now crossed over from being spontaneous to being at equilibrium):

`-(DeltaG_"rxn"^@(T^@))/(DeltaH_"rxn"^@T^@) = 1/T_"nonspont." - 1/T^@`

`1/T^@ - (DeltaG_"rxn"^@(T^@))/(DeltaH_"rxn"^@T^@) = 1/T_"nonspont."`

`=> color(blue)(T_"nonspont.") = [1/T^@ - (DeltaG_"rxn"^@(T^@))/(DeltaH_"rxn"^@T^@)]^(-1) = (1/T^@)^(-1)[1 - (DeltaG_"rxn"^@(T^@))/(DeltaH_"rxn"^@)]^(-1)`

`= T^@[1 - (DeltaG_"rxn"^@(T^@))/(DeltaH_"rxn"^@)]^(-1) = ("298.15 K")[1 - (-"141.1 kJ/mol")/(-"174.4 kJ/mol")]^(-1)`

`=` `color(blue)("1561.5 K")`

and you can see the two approaches essentially give the same result (`0%` error if you keep all your decimal places in your calculator).