Are octonions numbers?
What makes a number a number and not just an algebraic object? This question is an opportunity for thinking about such foundational questions.
What makes a number a number and not just an algebraic object? This question is an opportunity for thinking about such foundational questions.
1 Answer
I vote yes, but you are invited to agree or disagree.
Explanation:
The Octonions are sometimes called the "Cayley Algebra" and sometimes the "Cayley Numbers".
They are an extension of the Real numbers, closed under addition, multiplication, additive inverse and multiplicative inverse of non-zero elements. Addition of octonions is commutative and associative. Multiplication is generally neither commutative nor associative. They have no zero divisors. That is, if
Octonions are an extension of the Quaternions, which are an extension of the Complex numbers, which are an extension of the Real numbers.
But what do we mean by calling algebraic objects numbers and why might the octonions qualify?
In the following table are some properties of the real numbers
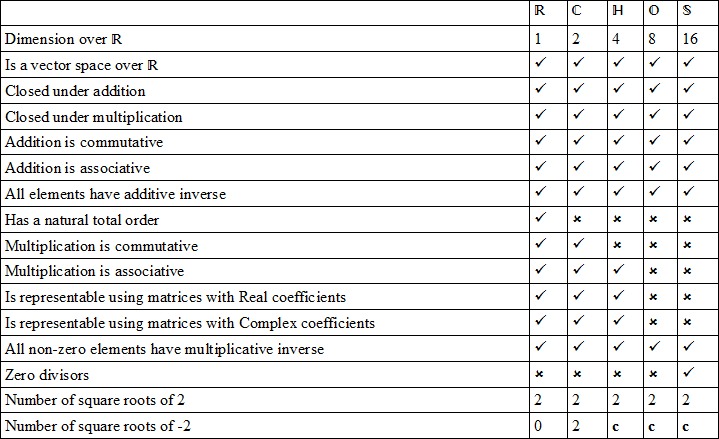
Note that
So Real numbers are well behaved and totally ordered, but algebraically incomplete in that they contain no solution to
Complex numbers are well behaved and algebraically complete, but have no natural ordering. A polynomial of degree
Quaternions have non-commutative multiplication, but are otherwise well behaved. Most polynomials will have an infinite number of quaternion valued zeros. Quaternions are useful for modelling 3 dimensional mechanical systems. Any quaternion can be written in the form
Octonions drop the requirement that multiplication be associative. Octonion multiplication does satisfy a weaker condition expressed as saying that multiplication is alternative. Octonions have applications in string theory, special relativity and quantum logic. Any octonion can be written in the form
To multiply octonions, you can use distributivity of multiplication over addition and the following multiplication table for the units
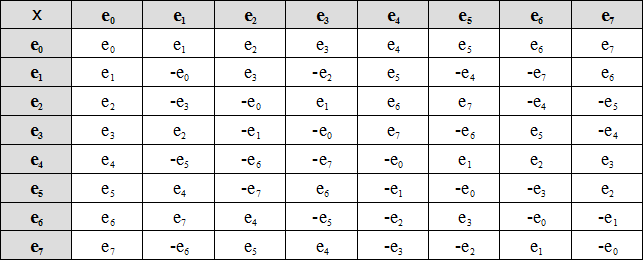
The octonions can be further extended using the Cayley-Dickson construction to form the sedenions - a 16 dimensional algebra over the Reals. Multiplication of sedenions is not even alternative and sedenions have zero divisors. The sedenions seem to have limited use, but one or two interesting properties.
My vote is that Octonions deserve to be called numbers, since they have fairly well defined arithmetic properties and multiple physical applications.

