Are there any geometric isomers of the stable octahedral complex [Co(NH3)3(NO2)3]? If there are, how many?
2 Answers
Facial and meridional isomers are possible with respect to the octahedral complex.
Explanation:
The
You could use the Bailar method, gone through in detail here, to determine how many isomers there are, as it is more generalized for all octahedral complexes.
However, since we have a
THE FAC ISOMER
The fac (facial) isomer has the three identical ligands aligned such that there is a
What I had just said can be drawn as follows:

So you can see that if you rotate the molecule about that
Furthermore, you can find a mirror plane that coincides with an
Therefore, the fac isomer is NOT an enantiomeric isomer and is the only fac isomer there is.
THE MER ISOMER
The mer (meridian) isomer has three
In essence, I switched the top-axial
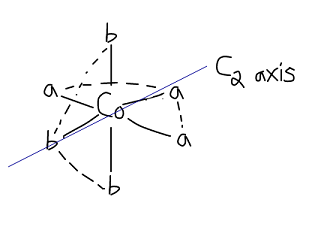
So you can see that if you rotate the molecule about that
Furthermore, you can find a mirror plane that is coplanar with the
Therefore, the mer isomer is NOT an enantiomeric isomer and is the only mer isomer there is.
CHECKING THE RESULT
In fact, if you look at the following table, the
Inorganic Chemistry, Miessler et al., pg. 326
Since a geometric isomer has the same connectivity but different spatial orientations, these stereoisomers, which agree with that definition, are also geometric isomers!
Thus, we have all geometric isomers identified.


