Are there more than one way to convert Polar to Rectangular coordinates?
1 Answer
Jan 14, 2016
All Polar
Explanation:
There may be many ways to visualize the conversion of Polar to Rectangular coordinates. Sometimes (depending upon the values of
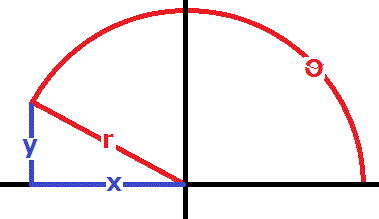
(I assume here that we are dealing only with Real values of
