Assuming human skin is at 98.6 degrees Fahrenheit, what wavelength is the peak in the human thermal radiation spectrum? What type of waves are these?
2 Answers
Explanation:
Wien's displacement law states that the black-body radiation curve for different temperatures peaks at a wavelength inversely proportional to the temperature.
where b is Wien's displacement constant, equal to
plugging this into our equation, we get the peak wavelength of radiated light:
This is in the range of what is called infrared radiation.
Should be the infrared fingerprint region.
We have a relationship for this called Wien's Displacement Law:
#\mathbf(lambda_max = b/T)# where:
#b = 2.89777xx10^(-3)# #"m"cdot"K"# is a proportionality constant, probably experimentally determined.#T# is temperature in#"K"# .#lambda_max# is the wavelength that you observe at its largest spectral energy density.
The spectral energy density is depicted in the following diagram, with respect to wavelength in
You can think of the spectral energy density as being proportional to the contribution of each wavelength range to some final observed color at a particular temperature. You can see that the peaks would correspond to
Converting temperature to
#(98.6^@ "F" - 32) xx 5/9 = 37^@ "C"#
#37 + 273.15 ~~ color(green)("310.15 K")#
And now we get a max wavelength of:
#lambda_max = (2.89777xx10^(-3) "m"cdotcancel"K")/("310.15" cancel"K")#
#= 9.343xx10^(-6) "m"#
Converting this to
#= 9.343xx10^(-6) cancel("m") xx (10^6 mu"m")/(1 cancel"m")#
#= color(blue)(9.343)# #color(blue)(mu"m")#
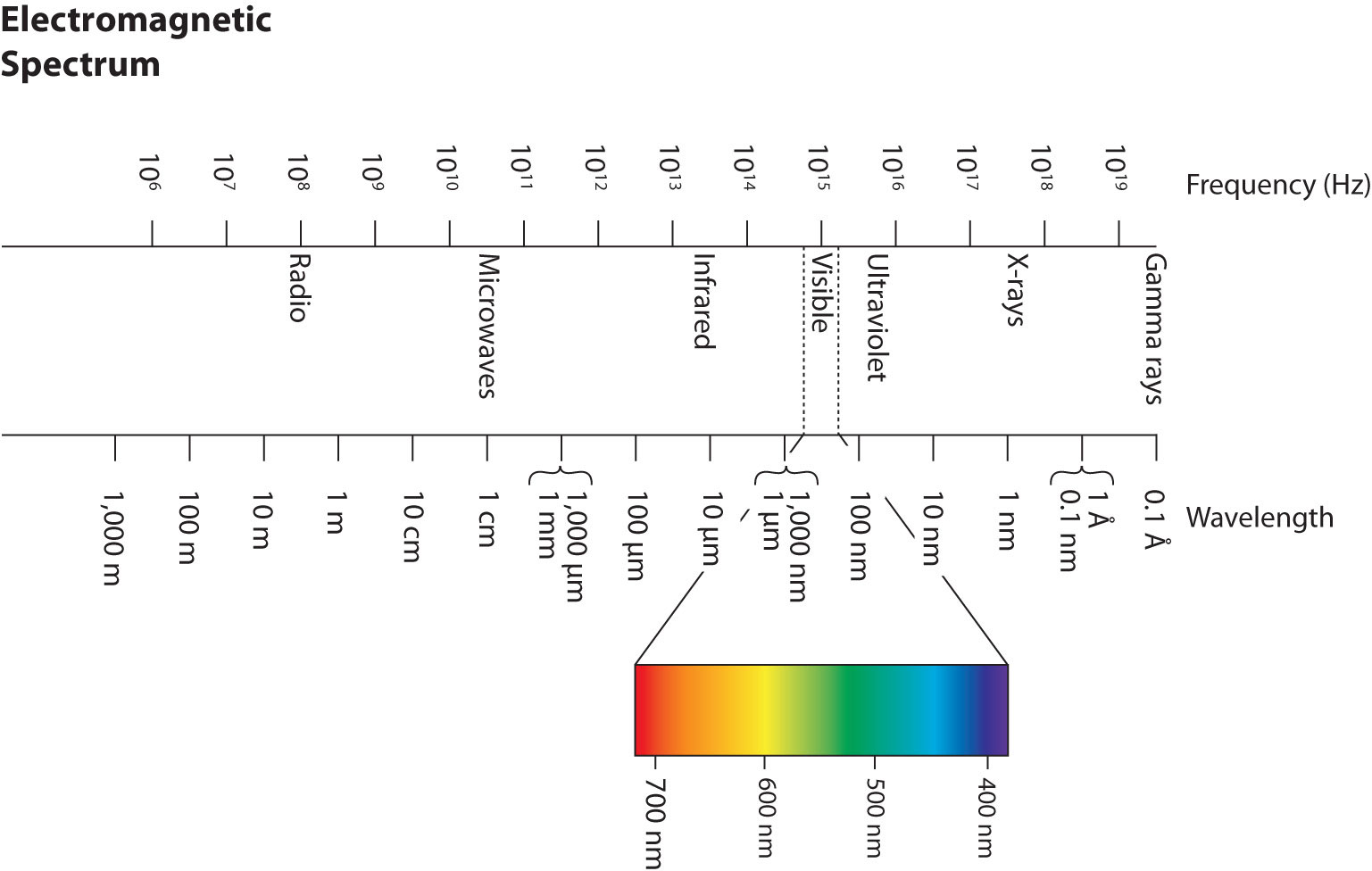
Being close to


