Calculate pH for a solution prepared by mixing 25ml of 0.1 M HCl with 25ml of 0.2 M NH3.What is the color of the solution if three drops of phenolphthalein is added to the solution?
1 Answer
Pale to bright pink.
Explanation:
Your starting point here will be the balanced chemical equation for this neutralization reaction
#"HCl"_text((aq]) + "NH"_text(3(aq]) -> "NH"_text(4(aq])^(+) + "Cl"_text((aq])^(-)#
Keep in mind, you're mixing hydrochloric acid, strong acid, and ammonia, a weak base, which means that even if the neutralization is complete, the pH of the resulting solution will not be equal to
So, your goal here is to determine if mixing the given solutions will result in a complete neutralization.
As you can see, hydrochloric acid and ammonia react in a
Use the molarities and volumes of the two solutions to determine how many moles of each you're adding to the final solution
#color(blue)(c = n/V implies n = c * V)#
#n_(HCl) = "0.1 M" * 25 * 10^(-3)"L" = "0.0025 moles HCl"#
#n_(NH_3) = "0.2 M" * 25 * 10^(-3)"L" = "0.0050 moles NH"_3#
Since you have twice as many moles of ammonia than you have of hydrochloric acid, you can conclude that the acid will act as a limiting reagent, i.e. it will be completely consumed by the reaction.
Now, since you have a
So, if
#n_(NH_4^(+)) = "0.0025 moles"#
of ammonium ions.
This means that after the reaction is complete, the solution will contain
#n_(HCl) = 0 -># completely consumed
#n_(NH_3) = "0.0050 moles" - "0.0025 moles" = "0.0025 moles NH"_3#
#n_(NH_4^(+)) = "0.0025 moles NH"_4^(+)#
You now have a solution that contains a weak base and its conjugate acid
The total volume of the solution will be
#V_"total" = V_(HCl) + V_(NH_3)#
#V_"total" = "25 mL" + "25 mL" = "50 mL"#
This means that the concentration of ammonia and of ammonium ions in the resulting solution will be
#["NH"_3] = ["NH"_4^(+)] = "0.0025 moles"/(50 * 10^(-3)"L") = "0.050 M"#
Before moving on, look for the base dissociation constant,
#K_b = 1.8 * 10^(-5)#
http://faculty.ncc.edu/LinkClick.aspx?fileticket=ZxmmjQwsn1w%3D&tabid=1900
As you know the pH of a buffer that contains a weak base and its conjugate acid can be determined using the solution's pOH, which is given by the Henderson - Hasselbalch equation
#color(blue)("pOH" = pK_b + log( (["conjugate acid"])/(["weak base"])))#
Even without doing any calculation, you can look at this equation and say that when you have equal concentrations of weak base and conjugate acid, the pOH of the solution will be equal to
#["NH"_4^(+)] = ["NH"_3] implies log( (["NH"_4^(+)])/(["NH"_3])) = 0#
Since
#color(blue)(pk_b = - log(K_b))#
you will have
#"pOH" = - log(1.8 * 10^(-5)) = 4.74#
The pH of the buffer will thus be
#color(blue)("pH" + "pOH" = 14)#
#"pH" = 14 - 4.74 = color(green)(9.26)#
Now, phenolphthalein, itself a weak acid, is an indicator that is colorless at pH values that are below
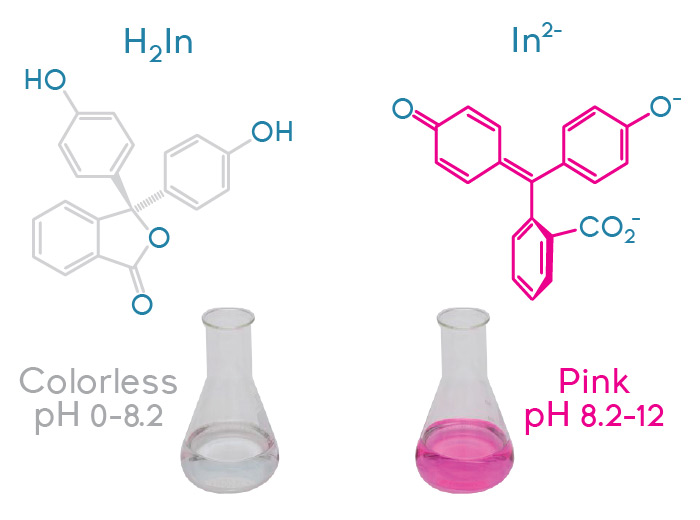
The half-way stage, where you have equal amounts of phenolphthalein and ionized phenolphthalein, takes place at a pH of about
That happens because mixing colorless and pink will simply get you a pale shade of pink.

