Calculate the concentration of each species at equilibrium?
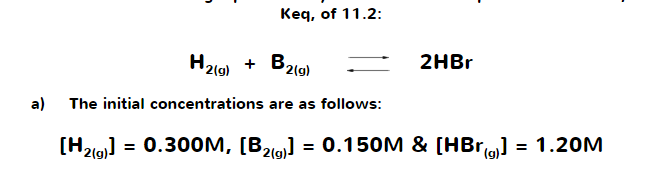
Given the initial concentration of HBr, does the same rule still applies in terms of ICE tables? I used the ICE TABLE but I am unable to calculate the concentrations.
Given the initial concentration of HBr, does the same rule still applies in terms of ICE tables? I used the ICE TABLE but I am unable to calculate the concentrations.
1 Answer
Here's what I got.
Explanation:
I'm not sure what you mean by
... the same rule still applies in terms of ICE tables?
but yes, an ICE table is what you need to use here in order to find the answer.
The problem provides you with the initial concentrations of hydrogen gas,
Moreover, you also know the value of the equilibrium constant,
Notice that you have
Before moving on to the calculations, use the given values to calculate the reaction quotient,
#Q_c = (["HBr"]_t)/(["H"_2]_t * ["Br"_2]_t) -> # does not use equilibrium concentrations!
In your case, you have
#Q_c = 1.20^color(red)(2)/(0.300 * 0.150) = 32#
Now, because
Similarly, the equilibrium concentration of hydrogen bromide will be lower than its initial value.
Set up an ICE table using the initial concentrations
#" " "H"_ (2(g)) " "+" " "Br"_ (2(g)) rightleftharpoons " "color(red)(2)"HBr"_ ((g))#
By definition, the equilibrium constant will be equal to
#K_(eq) = (["HBr"]^color(red)(2))/(["H"_2] * ["Br"_2])#
In your case, this will be equal to
#K_(eq) = (1.20 - color(red)(2)x)^color(red)(2)/((0.300 + x) * (0.150 + x))#
#11.2 = (1.44 - 4.8 * x + 4x^2)/((0.045 + 0.450 * x + x^2)#
This will be equivalent to
#0.504 + 5.04 * x + 11.2 * x^2 = 1.44 - 4.8 * x + 4x^2#
Rearrange to quadratic form to find
#7.2 * x^2 + 9.84 * x -0.936 = 0#
Now, this quadratic equation will produce two solutions, one positive and one negative.
#x_1 = -1.456" "# and#" "x_2 = 0.0893#
Notice that in order to avoid having negative equilibrium concentrations for hydrogen gas and bromine gas, you must pick the positive value of
This means that the equilibrium concentrations of the three chemical species that take part in the reaction will be
#["H"_2] = 0.300 + 0.0893 = color(green)(bar(ul(|color(white)(a/a)color(black)("0.389 M")color(white)(a/a)|)))#
#["Br"_2] = 0.150 + 0.0893 = color(green)(bar(ul(|color(white)(a/a)color(black)("0.293 M")color(white)(a/a)|)))#
#["HBr"] = 1.20 - color(red)(2) * 0.0893 = color(green)(bar(ul(|color(white)(a/a)color(black)("1.02 M")color(white)(a/a)|)))#
The values are rounded to three sig figs.
Notice that the equilibrium concentration of hydrogen bromide is still higher than the equilibrium concentrations of hydrogen gas and bromine gas, as you would expect for an equilibrium for which

