Calculate the standard free energy change for the below reaction at 25 degrees Celsius?
#CH_4"(g)"+2O_2"(g)"\toCO_2"(g)"+2H_2O"(l)"#
#\DeltaG_{f,H_2O"(g)"}^{o}=-237.2"kJ"/"mol"#
#\DeltaG_{f,CO_2"(g)"}^{o}=-394.4"kJ"/"mol"#
#\DeltaG_{f,CH_4"(g)"}^{o}=-50.8"kJ"/"mol"#
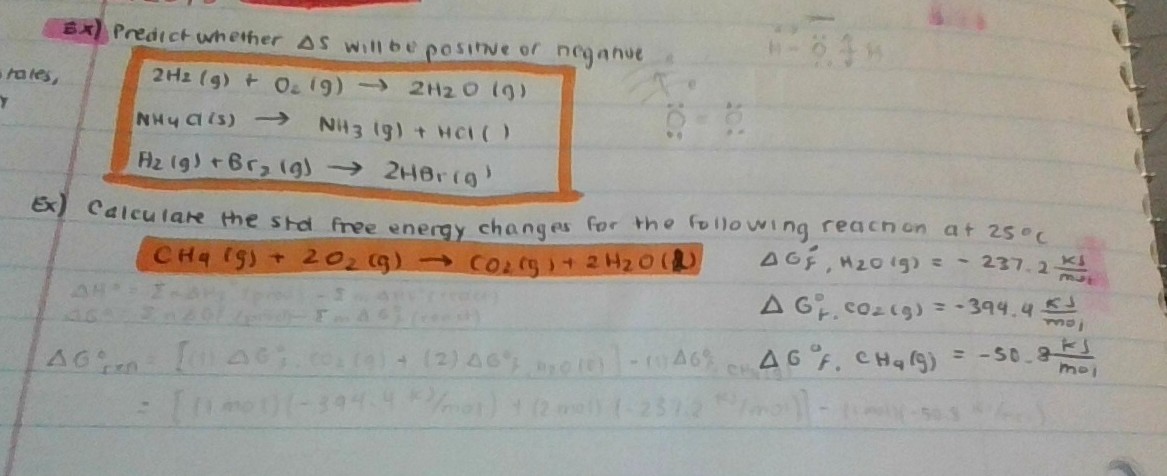
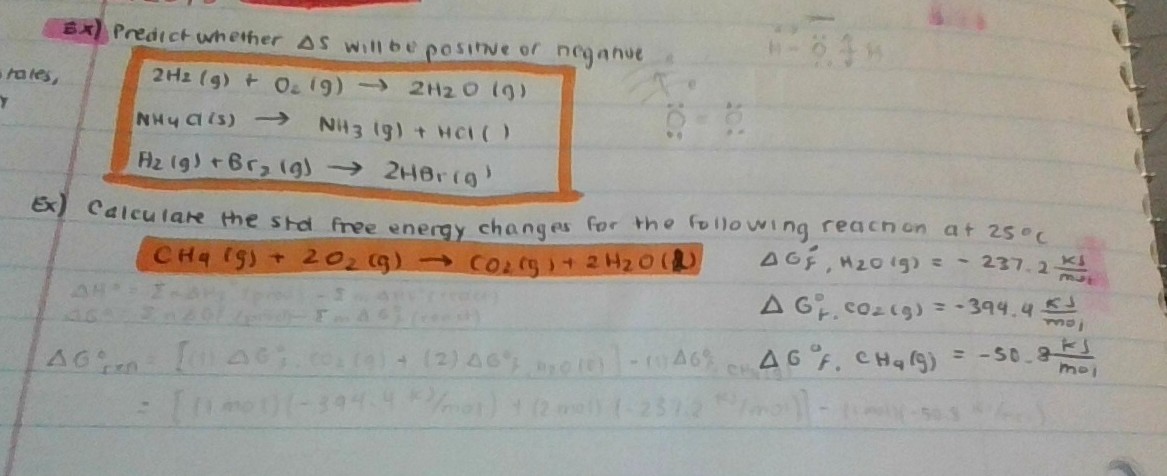
1 Answer
I'll assume these are all gases (in a coffee-cup calorimeter), although water liquid is possible in a bomb calorimeter. As a note, you should be especially careful that the values you look at are correct.
Here I get
Two things that can give you trouble are:
- What phase is the substance at
#25^@ "C"# and#"1 atm"# ?#DeltaG_f^@# for#"H"_2"O"(g)# is NOT the same as for#"H"_2"O"(l)# . - Is the substance in its standard state already, i.e. is
#DeltaG_f^@# for the substance ZERO?
Due to the fact that the Gibbs' free energy
#DeltaG_(rxn)^@ = sum_P n_P DeltaG_(f,P)^@ - sum_R n_RDeltaG_(f,R)^@# where
#DeltaG_f^@# is the change in Gibbs' free energy of reaction at#25^@ "C"# and#"1 atm"# in#"kJ/mol"# , and#P# and#R# are products and reactants.#n# is the mols of substance.
So, you take the sum over the products, sum over the reactants, and subtract the sums, making sure you get the phases correct, and the coefficients match up.
Also, the
Important standard state examples are:
#"H"_2(g), "C"(grap hite), "Al"(s), "P"_4(s), "S"_8(s)# (if you care, sulfur is actually orthorhombic in its standard state.) You should however definitely know that carbon graphite is the standard state of carbon, not diamond.)
The main diatomics to know here are
Therefore, for
#"CH"_4(g) + 2"O"_2(g) -> "CO"_2(g) + 2"H"_2"O"(g)#
we just have:
#color(blue)(DeltaG_(rxn)^@) = ["1 mol" cdot DeltaG_(f,CO_2(g))^@ + "2 mols" cdot DeltaG_(f,H_2O(g))^@] - ["1 mol" cdot DeltaG_(f,CH_4(g))^@ + "2 mols" cdot "0 kJ/mol O"_2(g)]#
#= ["1 mol" cdot -"394.4 kJ/mol CO"_2(g) + "2 mols" cdot -"237.2 kJ/mol H"_2"O"(g)] - ["1 mol" cdot -"50.8 kJ/mol CH"_4(g) + "2 mols" cdot "0 kJ/mol O"_2(g)]#
#=# #color(blue)(-"818 kJ")#

