CALCULUS RELATED RATE PROBLEM. PLEASE HELP??
A street light is mounted at the top of a 15-ft-tall pole. A man 6 ft tall walks away from the pole with a speed of 5ft/s along a straight path. How fast is the tip of the shadow moving when he is 40 ft from the pole?
A street light is mounted at the top of a 15-ft-tall pole. A man 6 ft tall walks away from the pole with a speed of 5ft/s along a straight path. How fast is the tip of the shadow moving when he is 40 ft from the pole?
1 Answer
The tip of the shadow is moving at a speed of
Explanation:
First, let's sketch the situation:
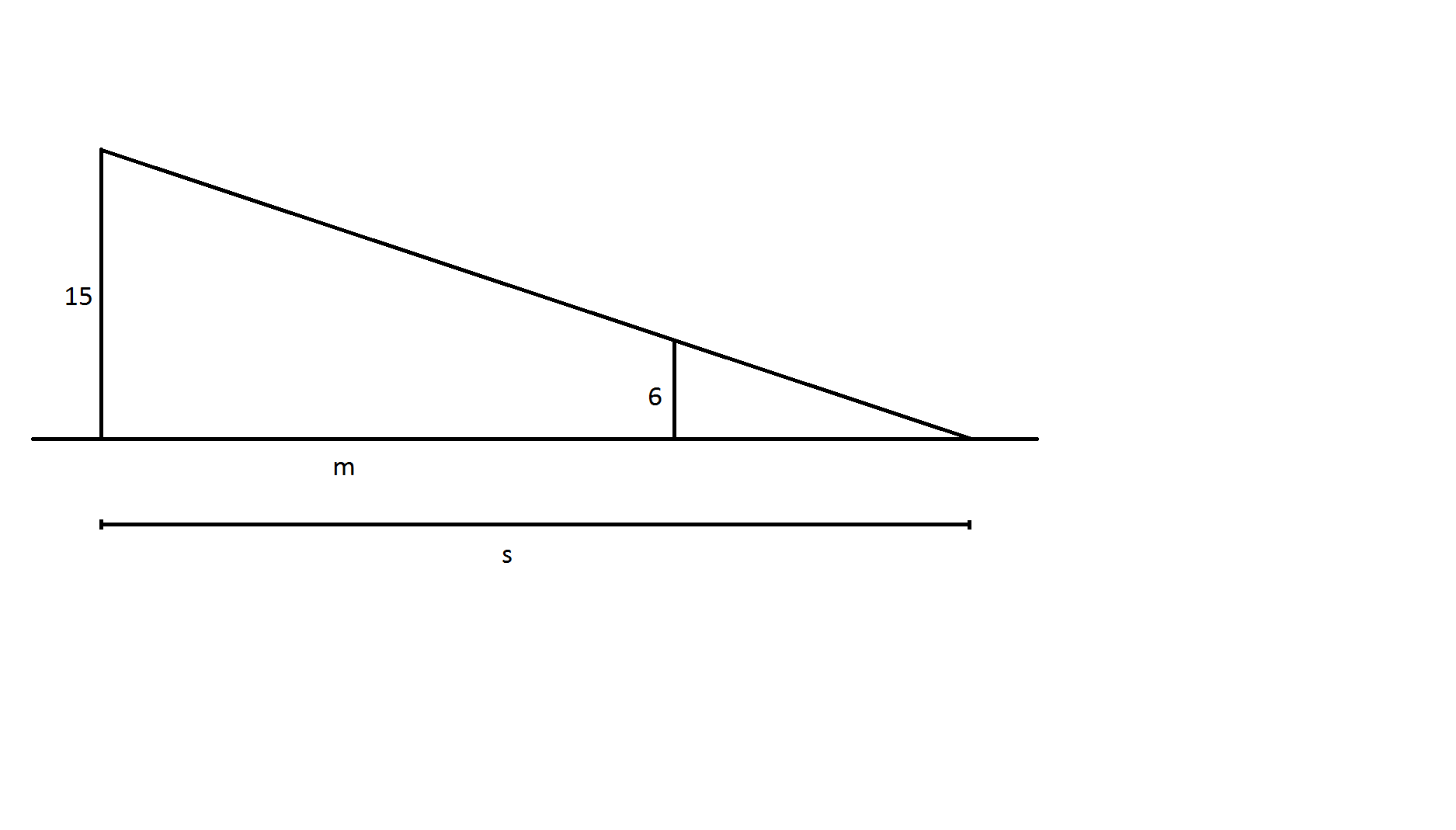
In the above image,
As derivatives are rates of change, we can rewrite our goal as trying to find
By the properties of similar triangles, we have
Differentiating with respect to time, we get
As it so happens, the rate of change of the tip of the shadow with respect to time is independent of the value of

