Can an asymptote be an inflection point?
2 Answers
Since an inflection point is a point on an equation, I assume you mean
"Can an asymptote intersect the line of an equation at an inflection point?"
Under current/modern usage of the concept of asymptote, the answer is a simple "yes";
for example,
Older, more traditional definitions of "asymptote" included a restriction that the equation could not cross the asymptote infinitely; so the given example would not be valid.
However it is possible to imagine a situation like that pictured below
which would still be valid under traditional definitions:
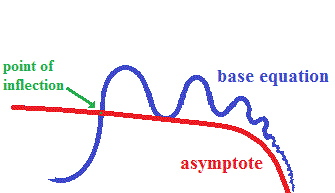
The function:
The graph of this function is concave down on
I have known students to incorrectly say that
Note that: an inflection point is a point on the graph where the concavity changes. There is no point of the graph of
As Alan P. said in his answer, a graph can have a point of inflection that lies on its asymptote.

