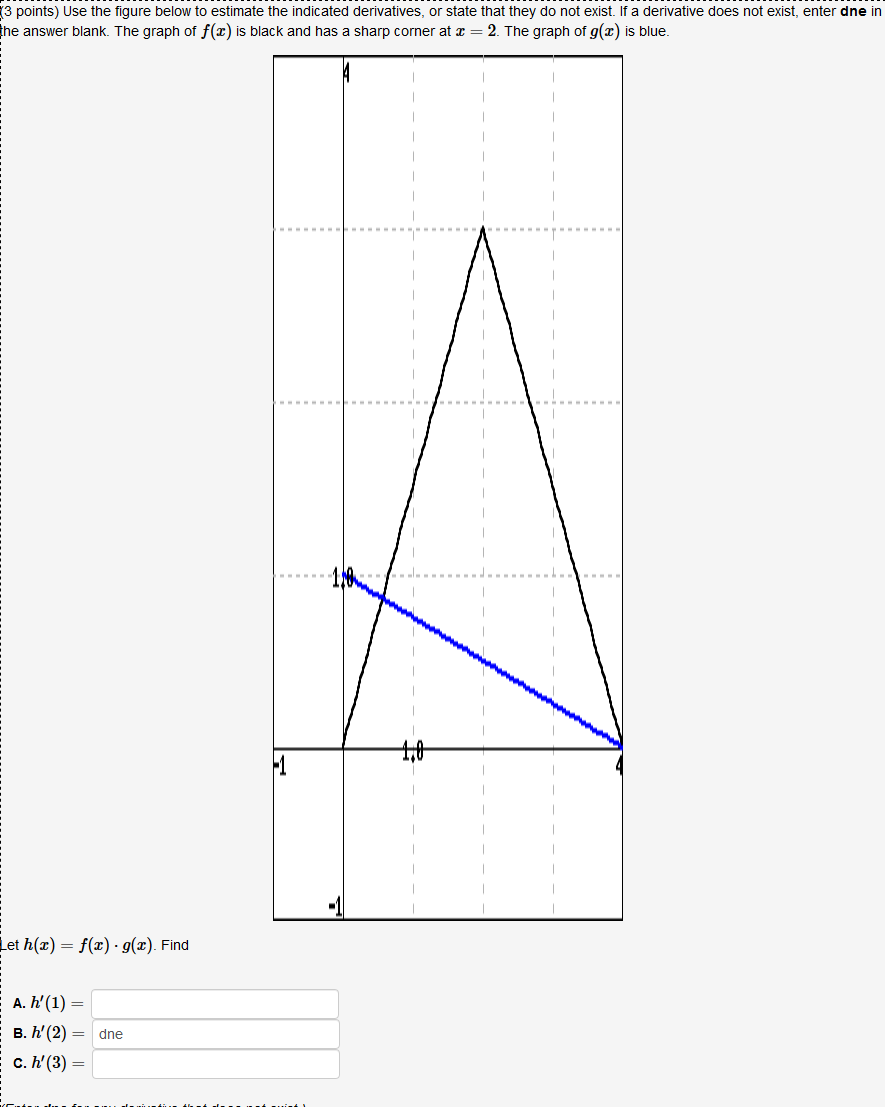
Can I get help with this graph? It involves derivatives and differentiation. I got h'(2) right but need help with h'(1) and h'(3)
1 Answer
Jun 13, 2018
Given that
Therefore
#h'(1) = f'(1)g(1) + f(1)g'(1)#
The values of
#f'(1) = (3 - 0)/(2- 0) = 3/2#
#g'(1) = (1 - 0)/(0 - 4) = -1/4#
To determine the values of
For f(x):
#y - 0 = 3/2(x - 0) -> y = 3/2x#
For g(x):#y - 1 = -1/4(x - 0) -> y = -1/4x + 1#
Therefore
#f(1) = 3/2(1)= 3/2#
#g(1) = -1/4(1) + 1 = 3/4#
Piecing all this together:
#h'(1) = 3/2(3/4) + (-1/4)(3/2) = 9/8 - 3/8 = 6/8 = 3/4#
The same process is required for
Hopefully this helps!

