Can someone explain this word problem?
1 Answer
Explanation:
Let's try to convert this into a more mathematical representation.
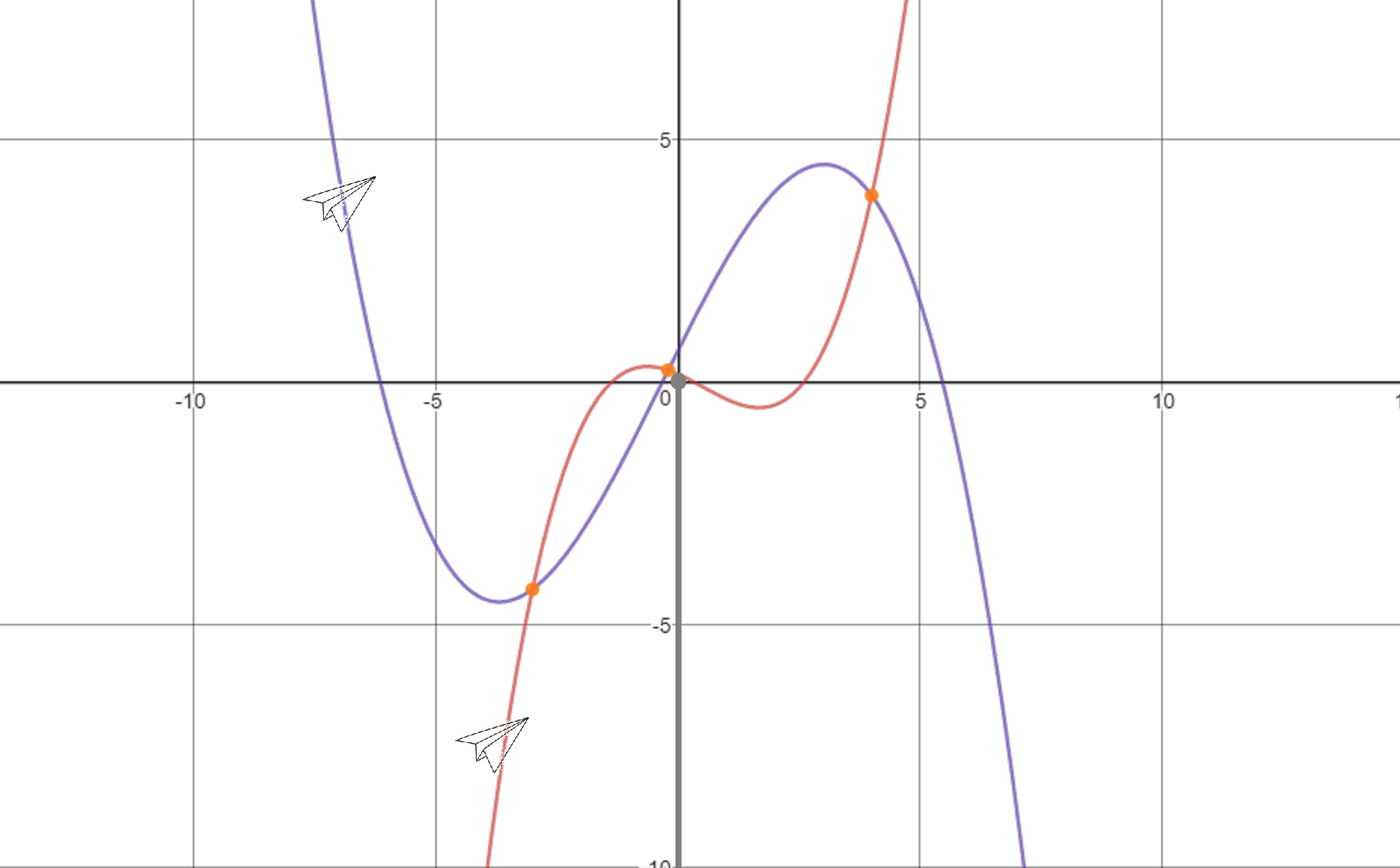
The positions of the planes are determined in relation to the top of a 10-metre pole: planes to the left and below the top of the pole are given negative x- and y- values and planes to the right and above the top of the pole are given positive x- and y- values.
The "x- and y- values" talk here is a big clue. This is describing a cartesian plane, with the origin (the
The path of Tyler's plane is modelled by f(x) = ..."
The path of Kym's plane is modelled by g(x) = ..."
As a point travels along a path on the cartesian plane, it forms a curve. As each plane flies along a path, and we are representing these planes as points, we can represent their flight paths as curves. In this case, we are given
Determine when f(x) > g(x).
After all that, it turns out we didn't really need to worry about all the setup to solve the problem. All we needed was
But all that aside, we can solve the inequality with only the last three sentences, which boil down to:
Solve for
While we're here, let's do that.
Letting
Our potential candidates are of the form
So we have
This inequality holds true when either all of the factors are positive, or two are negative and one is positive (the product of two negatives is a positive). If we check what happens to the factors as we traverse the real line, we get:
So, the solution to the inequality, and thus to the problem, is the union of the second and fourth intervals: