Question

Can someone help me with these two continuous function problems? Information is in the pictures.

Answer 1

`c=1`

`b=18`

Explanation:

For the first question we need to find the value of `c` such that:

`lim_(x->c^-)x^2-7=lim_(x->c^+)2x-8`

Since `f(x)` is expected to be the same approaching `c` from either side (by the definition of continuous) we can evaluate both limits by direct substitution:

`lim_(x->c^-)x^2-7=lim_(x->c^+)2x-8`

`->c^2-7=2c-8`

Now solve for `c`:

`c^2-2c+1=0`

`(c-1)^2=0 therefore c=1`

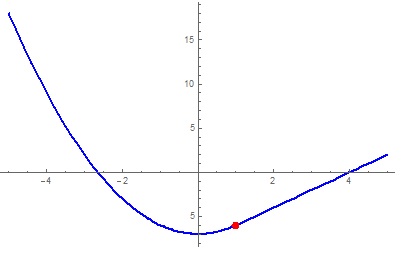
From the image it can be seen the graph is continuous when `c=1`. If we were to choose a value other than `c=1` then we would get a discontinuity. Say, for example, `c=0`:

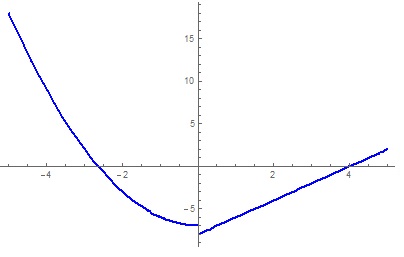
The graph is now clearly broken at `x=0` as the piecewise condition creates a jump in the value.

For the second part follow the same procedure:

`lim_(x->2^-)3x-4=lim_(x->2^+)-8x+b`

`3(2)-4=-8(2)+b`

`6-4=-16+b`

`-> b = 2+16=18`

Answer 2

`c = 1`
`b = 18`

Explanation:

to find out where one graph ends and another graph starts, you can use the point of intersection.

to find the `x-`coordinate for the point of intersection, find the value of `x` for which `y` is equal for both functions.

`x^2 - 7 = 2x - 8`

then solve for `x`:

`x^2 -2x - 7 = -8`

`x^2 - 2x + 1 = 0`

`(x-1)(x-1) = 0`

`x-1 = 0`

`x = 1` (repeated root)

the `y-`coordinate is `1^2 - 7 = 2 - 8 = -6`

hence, the point of intersection is

when `x<=1, f(x) = x^2 - 7`
when `x>1, f(x) = 2x - 8`

`c = 1`

this is the graph:

-

the inequalities `{x<=2}` and `x>2` show that the `x-`value of the point of intersection is `2`.

at `x=2`, `3x-4 = 6-4 = 2`

this means that `y = 2` at the point of intersection

therefore at `x=2, -8x + b = 2`

`2` can be substituted for `x` in solving for `b`:

`-8x + b = 2`

`b = 2 + 8x`

`b = 2 + 16`

`b = 18`

the point of intersection is `(2,2)`

to draw the graph:

draw the graph of `3x -4` up to the point `(2,2)`
from there, draw the graph `-8x + 18`

this is a digital representation: