Question

Can you give me examples of real numbers?

Answer 1

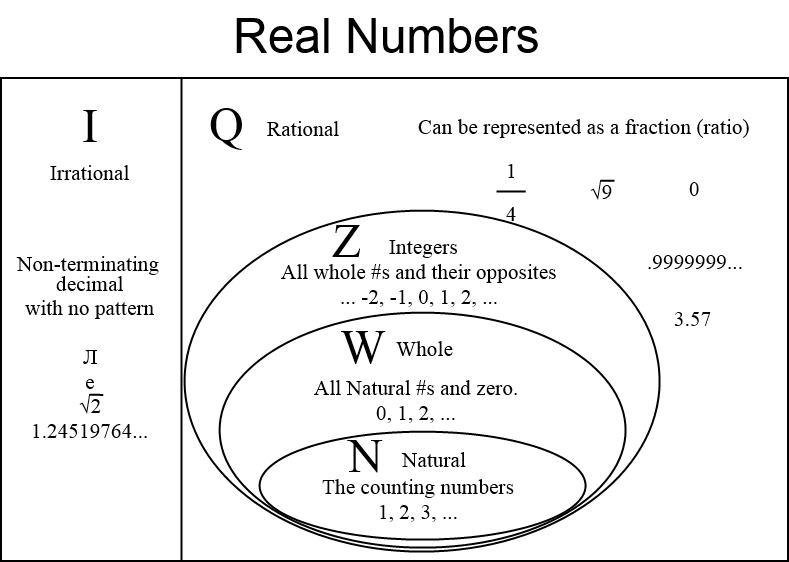
Until tenth grade, the set of real numbers is going to be the largest known to students. Commonly denoted `RR`, the real numbers contain the following sets:

`"The Natural Numbers: " NN = {1,2,3,...}`
`"The Whole Numbers: " W={0,1,2,3,...}=NN uu {0}`
`"The Integers: " ZZ = {...,-3,-2,-1,0,1,2,3,...}`
`"The rational numbers: " QQ = {p"/"q | p,q in ZZ}`
`"The irational numbers: " RR"\"QQ={x | x != p"/"q, p,q in ZZ}`

Note that there is no standard notation for some of these. Sometimes, the natural numbers include zero and the whole numbers are not needed. As such, there is no notation for the whole numbers. The one I gave, `W`, is the one I see most.

Rational numbers are a ratio of two integers. Numbers which can not be expressed as a ratio of two integers are called irrational, the set of which is denoted `RR"\"QQ` (the reals without the rationals) or `I`.

All natural and whole numbers are integers:

`NN sub ZZ and W sub ZZ`

All integers are rational numbers:

`ZZ sub QQ`

The rational and irrational numbers, together, form the real numbers:

`QQ uu RR"\"QQ = RR`

As such,

`RR = { x | x in QQ or x in RR"\"QQ }`

Another thing that defines rational numbers; they either have a terminating decimal or a repeating, non-terminating one:

`1"/"4 = 0.25`
`1"/"7 = 0.1428571428514285714285... = 0.bar(14285714285)`

The overlined sequence is repeating.

Irrational numbers are, simply, numbers which are not rational and dont have a terminating/repeating decimal. Famous example include:

`pi " "("The circle constant") ~~ 3.1415...`
`sqrt2 " "("Pythagoras' constant") ~~ 1.4142...`
`e " "("Euler's number") ~~ 2.7182...`