Can you solve the equation for this interval [0, 2pi]? Sin(2x-(pi/4)) = (sqrt2)/(2)
2 Answers
Here's how I did it:
Explanation:
First, we can rewrite this with an
From the unit circle, we know that
Add
There is still another solution since sine is also positive in the second quadrant:
To find the other solution, we refer to the unit circle:
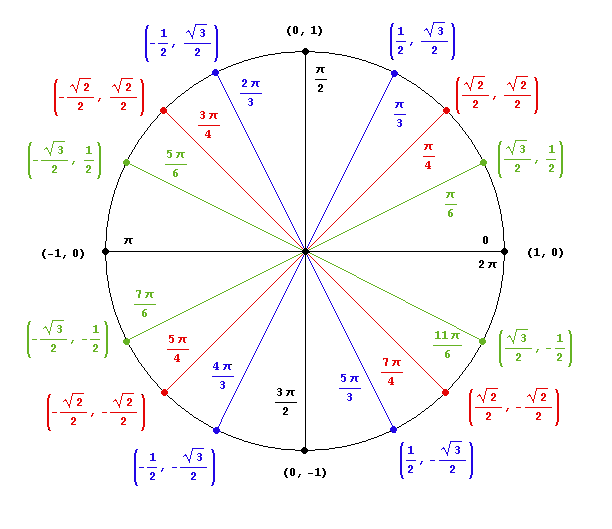
We can see that
So we have
However, we want the solutions between
First, we have to find the period of the function
The period is
This means that we can add
We cannot add another
So the final answers are
Hope this helps!
Explanation:
For:


