Question

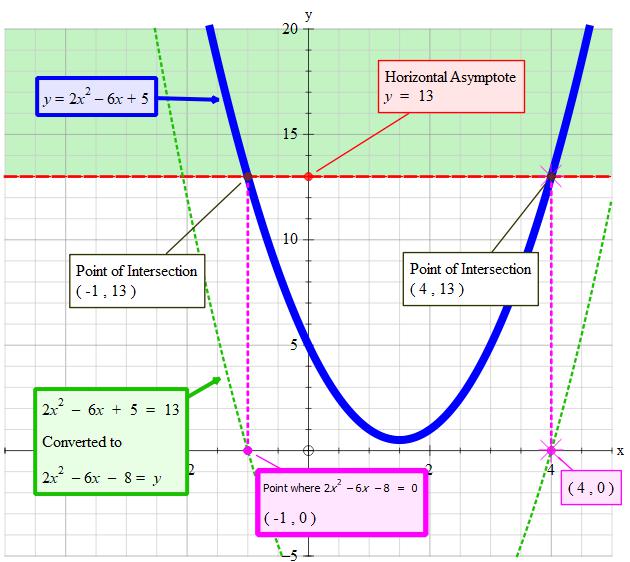
Can you tell that for example it's an equation `y=2x^2-6x+5` And question is to find the set values of x for which y>13 So in it answers are x<-1 and x>4 How do we know that x is greater or less than -1 or 4 as when we solve it on calculator?

Answer 1

Please see below.

Explanation:

We have `y=2x^2-6x+5` and we seek values of `x` for which `y>13`

`y>13` means `2x^2-6x+5>13`

i.e. `2x^2-6x+5-13>0`

or `2x^2-6x-8>0`

or `x^2-3x-4>0`

or `(x-4)(x+1)>0`

This means product of `(x-4)` and `(x+1)` is positive.

This has two possibilities

One when both are positive i.e. `x-4>0` and `x+1>0` and in other words `x>4` and `x>-1`. This is possible only when `x>4`

Other possibility is when both are negative i.e. `x-4<0` and `x+1<0` and in other words `x<4` and `x<-1`. This is possible only when `x<-1`

Hence `y>13`, when either `x<-1` or when `x>4`

In fact if we draw graph of `y=2x^2-6x+5`, we see that `y>13` when either `x<-1` or when `x>4`

graph{(2x^2-6x+5-y)(y-13)=0 [-3.75, 6.25, 10.1, 15.1]}

Answer 2

See explanation

Explanation:

set `2x^2-6x+5=y>13`

As the `2x^2` is positive then the graph is of general shape `uu`

By changing the above from > to = we can solve for the points where `y` is just starting to be `y>13`

To find the critical points write `2x^2-6x+5=13` as:

`2x^2-6x+5-13=0`

The required `x` values will be where `x` satisfies `2x^2-6x+5-13=0`

`2x^2-6x-8=0" "` I happen to spot this this can be factorised

`(2x+2)(x-4) = 0`

For this to work we have `(2x+2)=0` or `(x-4)=0`

Thus we have `color(red)(x=-1" or "x=+4)` as the critical points. So These x-values are the points where `2x^2-6x+5=y=13`

So for `2x^2-6x+5>13` we have to look at the the `x's` for making `y>13` and these are: `color(green)(x<-1 and x>4)`
`color(white)("dddddddddddddddddddddddddddddddddd")color(red)(uarr)`
`color(white)("ddddddddddddddddddddd")color(red)("Corrected "x>14" to "x>4)`