Question

Circle A has a center at `(2 ,3 )` and an area of `12 pi`. Circle B has a center at `(8 ,2 )` and an area of `66 pi`. Do the circles overlap?

Answer 1

Yes, they do.

Explanation:

We have to determine the radiuses of the circles.

Recall that the area of a circle is given by `a = r^2pi`.

`color(blue)("A"_"circle A" = r^2pi`

`color(blue)(12π = r^2pi`

`color(blue)(r = sqrt(12) = 2sqrt(3)`

`color(red)("A"_"circle B" = r^2pi)`

`color(red)(66pi = r^2pi`

`color(red)(r = sqrt(66))`

Now, let's graph the circles on the following cartesian plane.

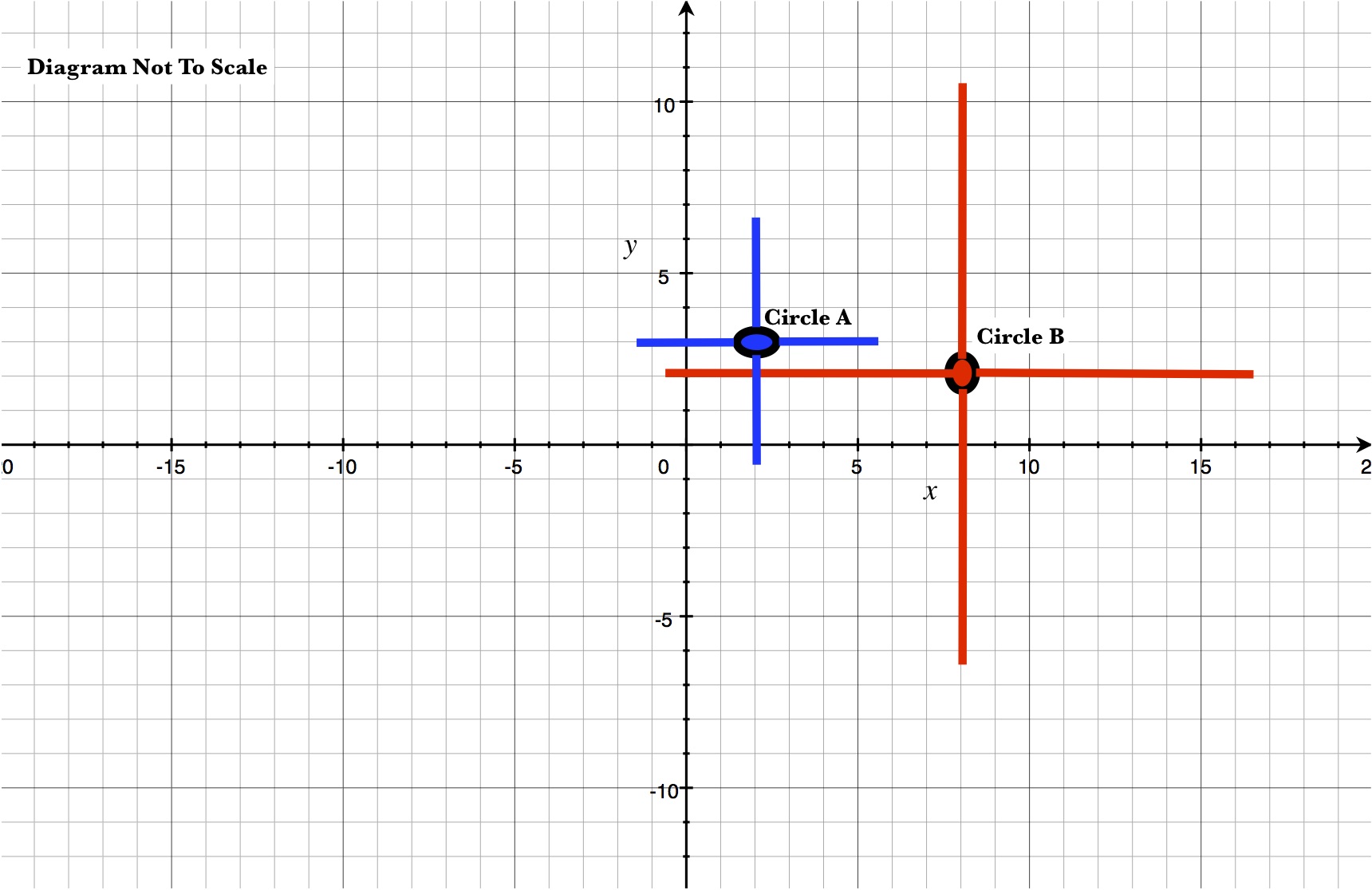
*The diagram above shows the length, approximately to scale, of the radiuses of both circles A and B in all directions from the center. For example, the image tells us that Circle B's radius enters circle A's radius. *

As was explained in the last paragraph, Circle A overlaps Circle B.

Hopefully this helps!