Circle A has a center at #(2 ,4 )# and an area of #81 pi#. Circle B has a center at #(4 ,3 )# and an area of #36 pi#. Do the circles overlap? If not, what is the shortest distance between them?

Question

1157 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2016-11-07T18:44:38

The larger circle completely encloses the smaller circle.

Here is a graph of the two circles:

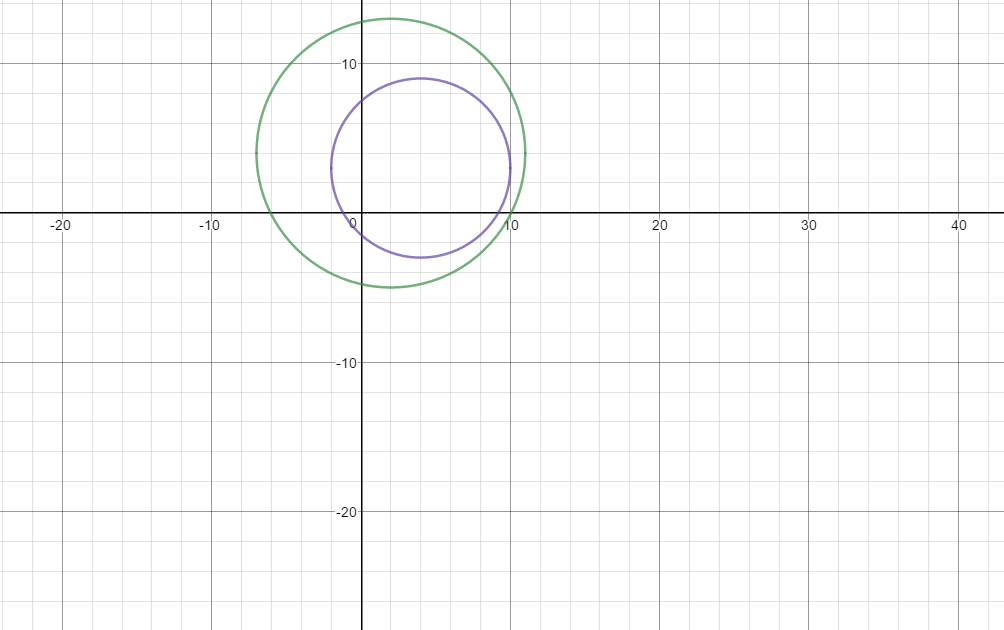
enter image source here

Answer 2 · 2016-11-08T06:25:19

Smaller circle lies within bigger circle. Smallest distance between them is #0.764#

Circle A has a center at #(2,4)# and its radius is #sqrt((81pi)/pi)=9#

Circle B has a center at #(4,3)# and its radius is #sqrt((36pi)/pi)=6#

The distance between centers is

#sqrt((4-2)^2+(3-4)^2)=sqrt(2^2+1^2)=sqrt5#

As the distance at #sqrt5# between them is less than difference in radius which is #9-6=3#

smaller circle lies within bigger circle. For details see here

Also see graph below (the other answer).

Smallest distance between them is #9-6-sqrt5=0.764#