Question

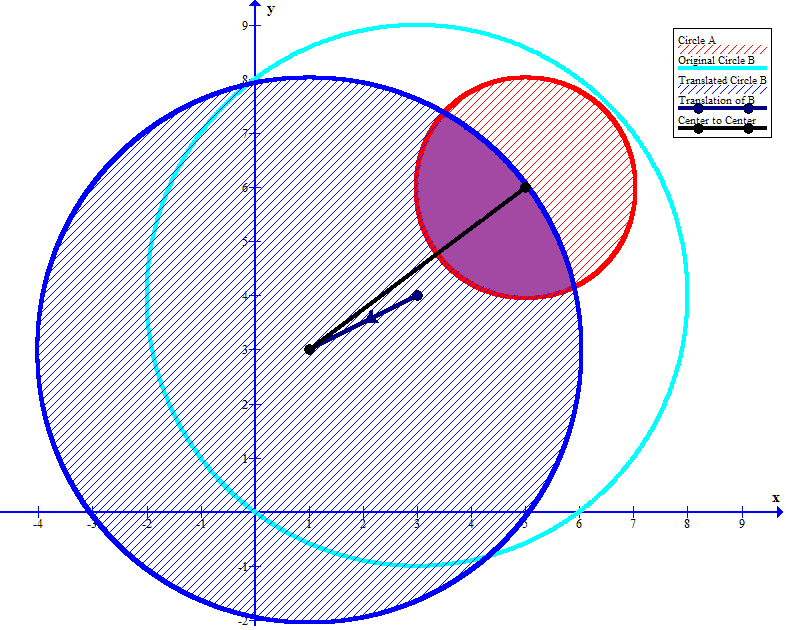
Circle A has a radius of `2` and a center at `(5 ,6 )`. Circle B has a radius of `5` and a center at `(3 ,4 )`. If circle B is translated by `<-2 ,1 >`, does it overlap circle A? If not, what is the minimum distance between points on both circles?

Answer 1

The circles overlap.

Explanation:

If circle `B` with center `(3,4)` is translated by `<-2,1>` its new center will be at `(3-2,4+1)=(1,5)`
The distance between the center of `A` at `(5,6)` and the new center of `B` is given by the Pythagorean Theorem as:
`color(white)("XXX")d=sqrt((5-1)^2+(6-5)^2)=sqrt(17)~~4.123`

We are told that circle `A` has a radius of `2` and circle `B` has a radius of `2` and circle `B` has a radius of `5`.

Considering the line segment joining the centers of the two circles,
we can see that `A` covers `2` units of that line segment and `B` covers `5` units (actually more than the length of the line segment.

Since there is only `4.123` units between the two centers, the circles must overlap.