Circle A has a radius of 2 2 and a center of (3 ,1 )(3,1). Circle B has a radius of 6 6 and a center of (8 ,5 )(8,5). If circle B is translated by <-4 ,-1 ><−4,−1>, does it overlap circle A? If not, what is the minimum distance between points on both circles?
2 Answers
See process below
Explanation:
Equation for
Equation for
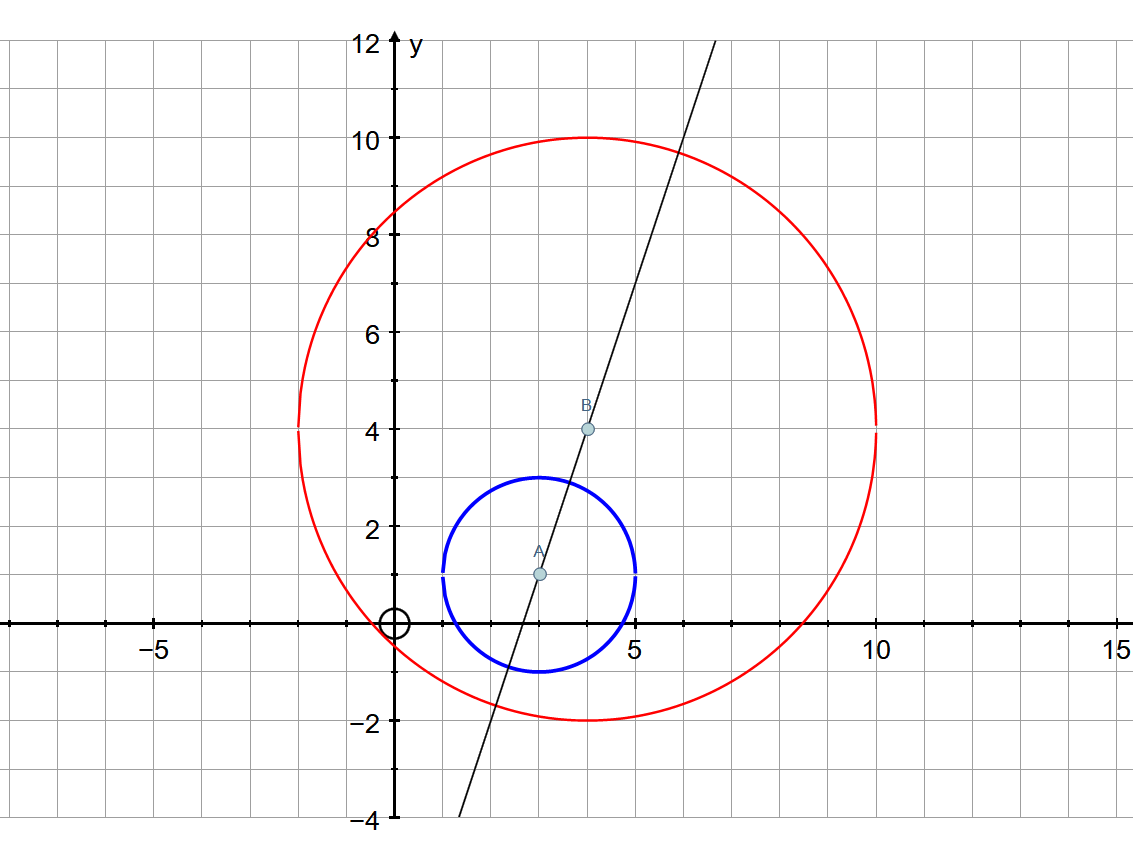
A traslation is a isometric transformation, then the image for B in this movement is other circle of radius 6 and center in
Obviously doesn`t overlap both circles and the minimum distance will lay in the line joining both centers
Lets calculate line equation
This line intercept to both circles in 4 points (see graph)
Distance is calculated by the standard formula (euclidean distance)
Lets see these points:
The minimum distance will be
Explanation:
The general equation of a circle is:
Where:
Circle A
If B is translated by
Centre:
Circle B:
By using the distance between the centres and the radii we can deduce the following:
Let:
If:
Using the distance formula:
Sum of radii:
So the circles intersect at two points or one is contained in the other. This can be tested by noticing that if the diameter of the smaller circle is less than the radius of the larger then the smaller circle is contained in the larger one.
Diameter of smaller circle is
Radius of larger circle is
So smaller circle is contained in the larger.
To find the shortest distance:
PLOT: