Circle A has a radius of #2 # and a center of #(6 ,5 )#. Circle B has a radius of #3 # and a center of #(2 ,4 )#. If circle B is translated by #<1 ,3 >#, does it overlap circle A? If not, what is the minimum distance between points on both circles?

Question

1590 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-10-10T18:04:21

Circle B overlaps circle A after translation.

If circle B is translated by <#1,3#>, the center will be (#2+1,4+3#)=(#3,7#).
Let circle B' has a radius of #3# and a center of (#3,7#).

The distance #d# between the center of circle A and that of circle B' is:
#d=sqrt((3-6)^2+(7-5)^2)=sqrt(13)#

Let #r_a# and #r_b# to the radius of circle A and circle B(and B') respectively. #r_a=2, r_b=3#.

This satisfies the inequation:
#abs(r_a-r_b)< d< r_a+r_b#

Therefore circle A and circle B' (translated circle B) do neither circumscribe nor inscribe. They overlap.
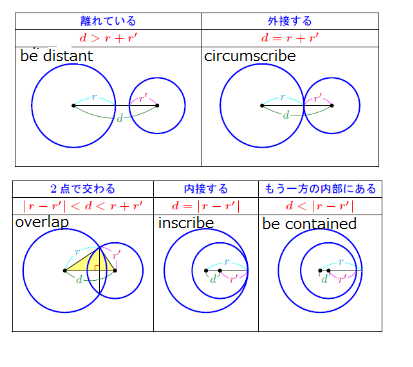
enter image source here
The figure is cited from http://examist.jp/mathematics/figure-circle/two-circle/ (Japanese)