Question

Circle A has a radius of `3` and a center of `(8 ,7 )`. Circle B has a radius of `2` and a center of `(6 ,1 )`. If circle B is translated by `<2 ,7 >`, does it overlap circle A? If not, what is the minimum distance between points on both circles?

Answer 1

Circles Overlap

Explanation:

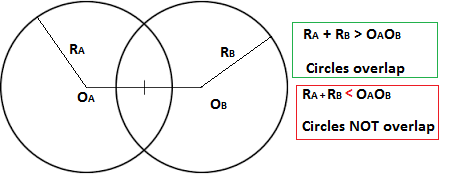
Given : `O_A ((8),(7)), R_A = 3, O_B ((6),(1)), R_B = 2`

`O_B` translated by `(2,7)`

New `O_B -> ((6+2),(1+7)) => ((8),(8))`

`vec(O_AO_B) = sqrt((8-8)^2 + (8-7)^2) = 1`

Sum of Radii `R_A + R_B = 3 + 2 = 5`

Since #R_A + R_B > vec(O_AO_B), both the circles overlap