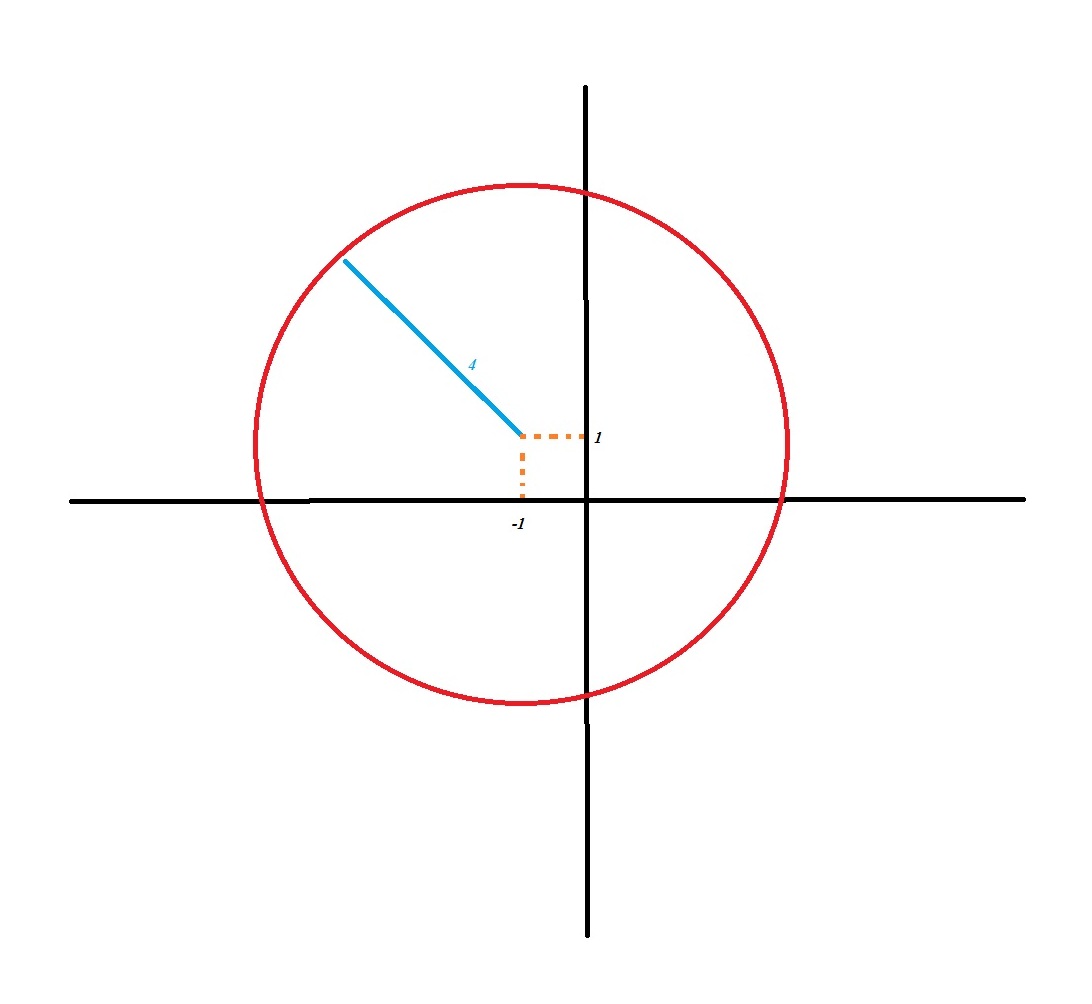
Circle has the equation #x^2+y^2+2x-2y-14=0#, how do you graph the circle using the center (h,k) radius r?
1 Answer
Dec 5, 2015
I found a circle centred at
Explanation:
I would write:
add and subtract some values:
or
Which is in the form:
giving you a circle centred at