What are common mistakes students make with ellipses in standard form?
2 Answers
The Standard form for an ellipse (as I teach it) looks like:
(h,k) is the center.
the distance "a" = how far right/left to move from the center to find the horizontal endpoints.
the distance "b" = how far up/down to move from the center to find the vertical endpoints.
I think that often students will mistakenly think that
Also, I think sometimes students mistakenly move up/down instead of right/left when applying these formulas to their problems.
Here is an example to talk about:
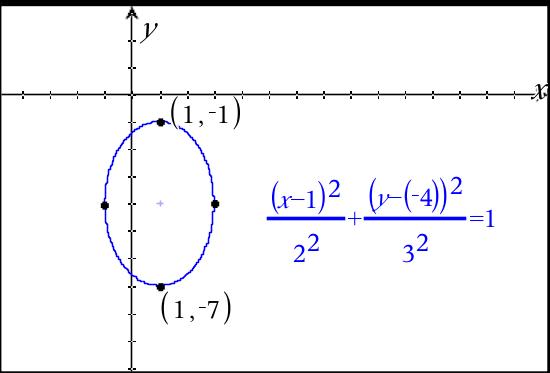
The center is (1, -4). You should move right and left "a" = 2 units to get the horizontal endpoints at (3, -4) and (-1, -4). (see image)
You should move up and down "b" = 3 units to get the vertical endpoints at (1, -1) and (1, -7). (see image)
Since a < b, the major axis is going to be in the vertical direction.
If a > b, the major axis will be going in the horizontal direction!
If you need to find out any other information about ellipses, ask another question!
(Confusion as to whether
Recall that the standard form for an ellipse centered at the origin is
Already, however, some will take issue with the formula listed above. Some schools of thought hold that
The same holds true with
Make sure you know which method your instructor (or the program you're using) prefers. If no strong preference exists, then simply decide for yourself, but be consistent with your decision. Changing your mind halfway through the assignment will make things unclear, and changing your mind halfway through a single problem will just lead to mistakes.
(Radius/axis confusion)
The majority of mistakes in ellipses seem to result from this confusion as to which radius is major and which is minor. Other possible mistakes can arise if one confuses the major radius with the major axis (or the minor radius with the minor axis). The major (or minor) axis is equal to twice the major (or minor) radius, as it is essentially the major (or minor) diameter. Depending on the step where this confusion occurs, this can lead to severe errors in scale for the ellipse.
(Radius/radius squared confusion)
A similar error occurs when students forget that the denominators (
(Hyperbola and Ellipse confusion) [WARNING: Answer is fairly lengthy]
Another relatively common mistake occurs if one mis-remembers the formula for the ellipse. Specifically, the most common of these errors seems to occur when one confuses the formula for ellipses with that for hyperbolas (which, recall, is
Specifically, recall that an ellipse is the locus of points related to two foci
By contrast, a hyperbola is the locus of points related to two foci in such a manner that, for a point
Relating to the definition of conic sections, the overall eccentricity


