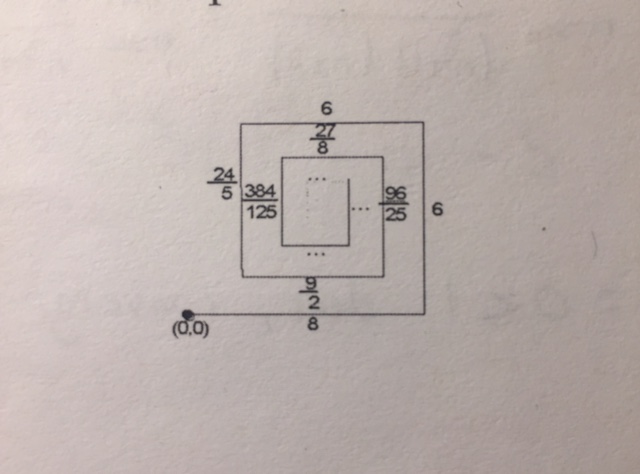
Consider a mobile moving along this path that starts at the point #(0,0)#. What are the coordinates of the point of arrival of the mobile ? (See image below)
A "Suits and Series" problem.

A "Suits and Series" problem.
1 Answer
Point of arrival is:
Explanation:
In the x-direction, defined as horizontal direction with positive direction being left to right:
This is an alternating geometric series.
The sum to infinity for a geometric series with
#S_oo = a/(1 - r)#
In the y-direction, defined as vertical direction with upward positive:
With the same reasoning:
Point of arrival is:

