Question

Consider the function defined by f(x)= sinx/x if `-1 <=x < 0`, ax+b if `0 < =x <= 1` and `(1-cosx)/x` if x >1, how do you determine a and b such that f(x) is continuous on [-1,2]?

Answer 1

`a = -cos1 ~~ = 0.540`
`b = 1`

Explanation:

Assuming we are working in radians.

We want our function, `f(x)` to be defined by:

`f(x) = { (sinx/x,-1 le x lt 0), (ax+b, 0 lt x le 1), ((1-cosx)/x, x gt 1) :}`

Let us denote each sub-function by `f_1(x), f_2(x)` and `f_3(x)` such that:

`f(x) = { (f_1(x)=sinx/x,-1 le x lt 0), (f_2(x)=ax+b, 0 lt x le 1), (f_3(x)=(1-cosx)/x, x gt 1) :}`

We can graph for illustrative purposes, `f_1(x)` and `f_3(x)` for the domain `x in RR`

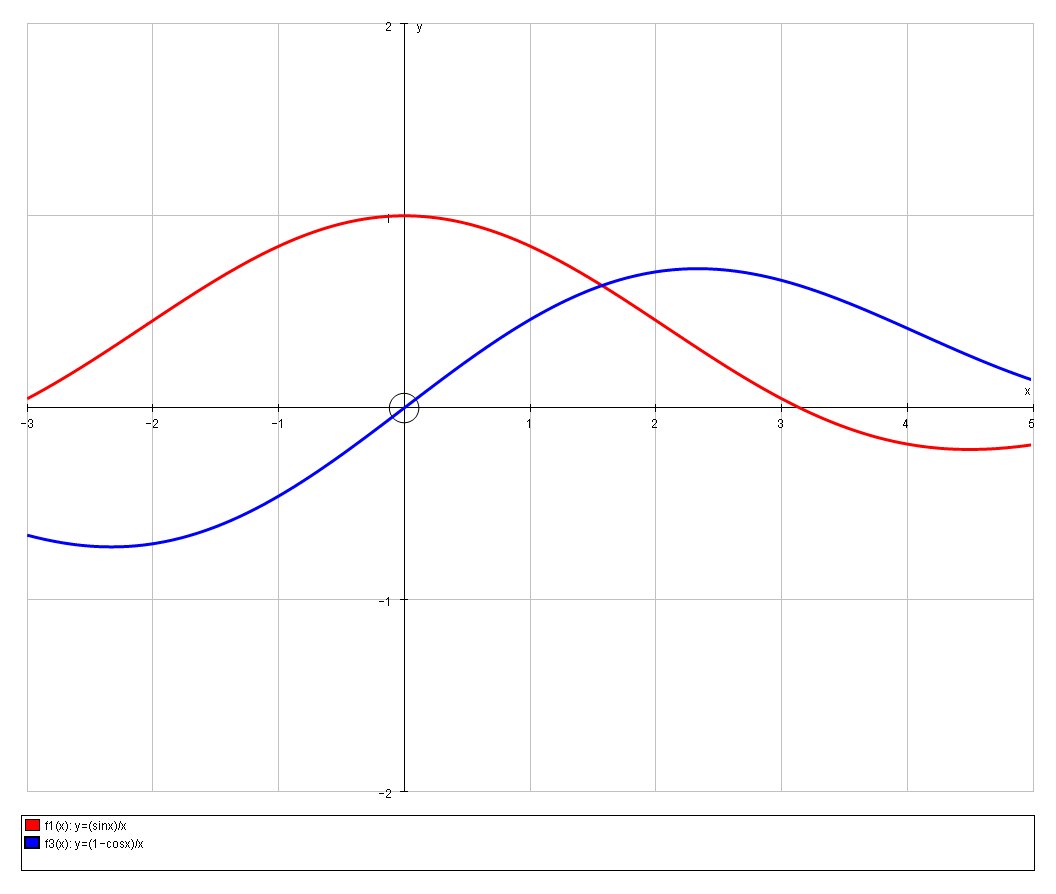
And we note that all three sub-functions are continuous in their own right.

If we now examine the functions `f_1(x)` and `f_1(x)` restricted to their appropriate domains we have:

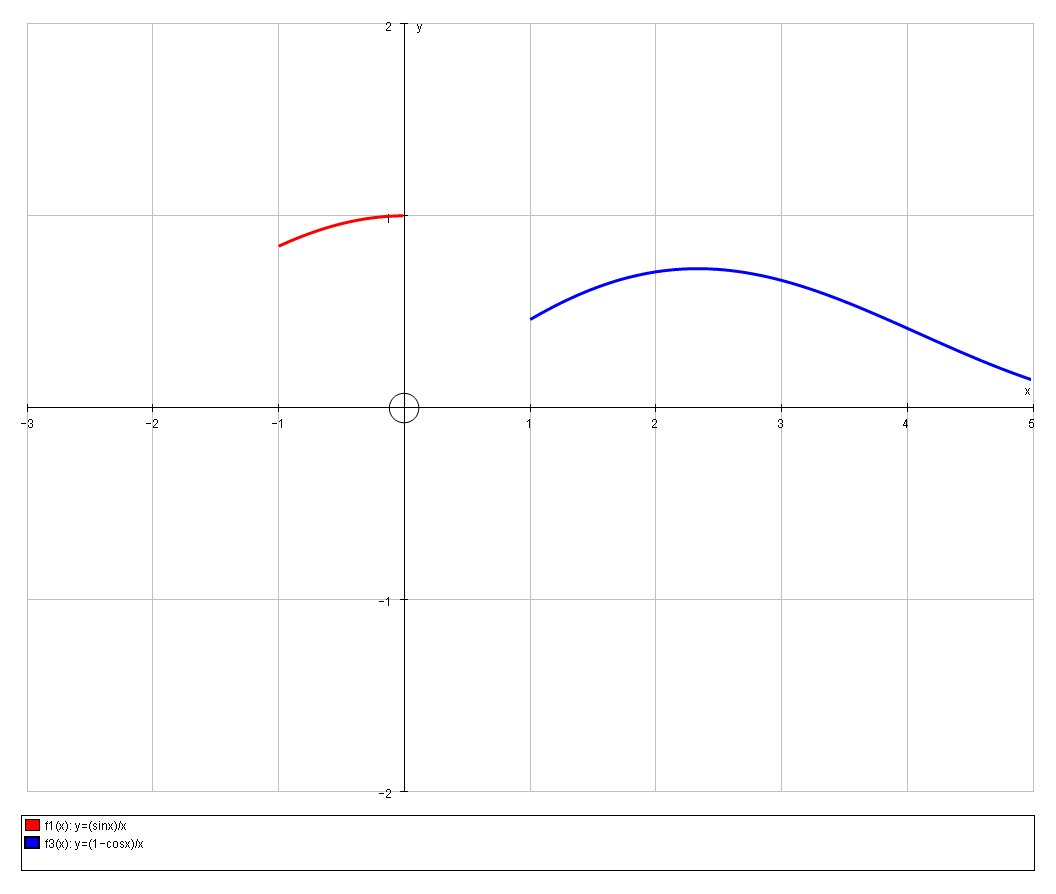
So, as we expected there is a discontinuity at the junctions between `f_1(x)` and `f_2(x)` and between `f_2(x)` and `f_3(x)` so as we require a linear function `ax+b` to complete the continuity we simply need to find the two coordinates associated with the discontinuity and find the unique equation of the straight line that [passes through those point.

Using some standard calculus trigonometry limits we have:

When `x=0 => f_1(x) = lim_(x rarr 0) sinx/x = 1`
When `x=1 => f_3(x) = lim_(x rarr 0) (1-cosx)/x = 1-cos1`

So the coordinates of the discontinuities are:

`(0,1)` and `(1,1-cos1)`

So using the straight line point/point equation:

`(y-y_1)/(y_2-y_1) = (x-x_1)/(x_2-x_1)`

then the equation we seek is:

`(y-1)/(1-cos1-1) = (x-0)/(1-0)`

`:. (y-1)/(-cos1) = x`
`:. y-1 = -xcos1`
`:. y = -xcos1+1`

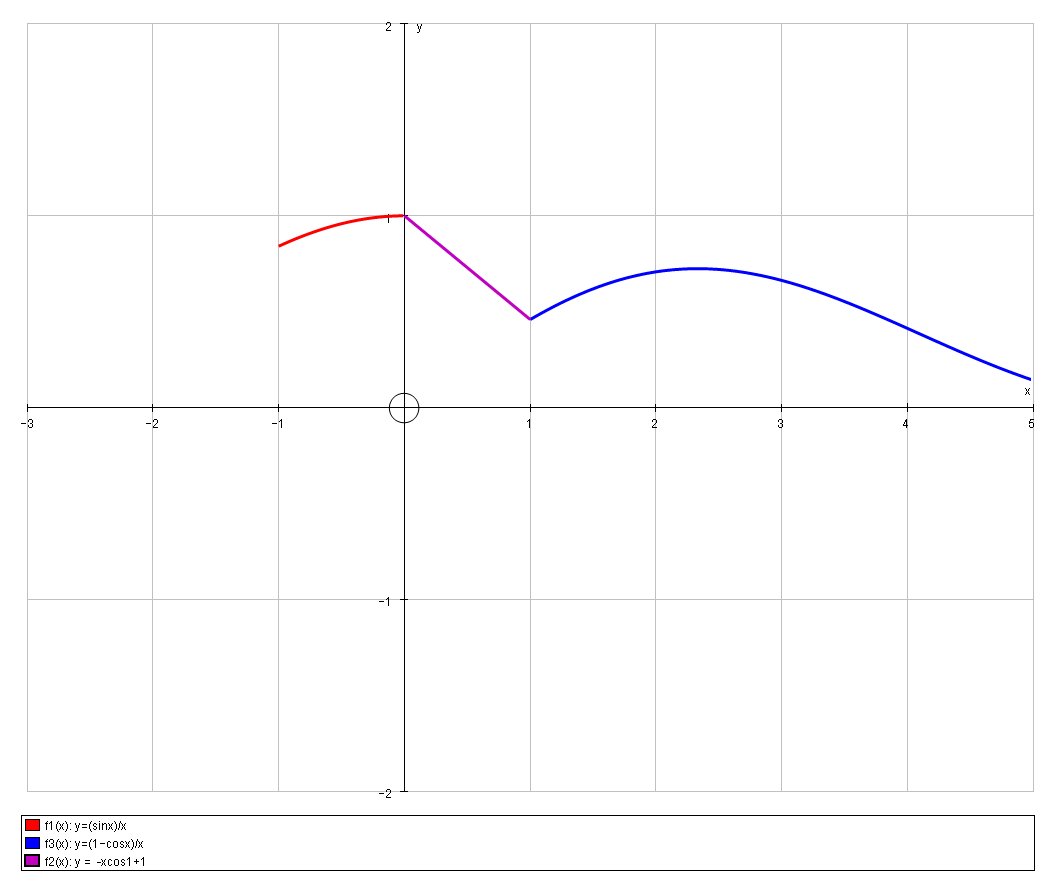
Thus comparing `y = -xcos1+1` with y=ax+b# we require:

`a = -cos1 ~~ = 0.540`
`b = 1`