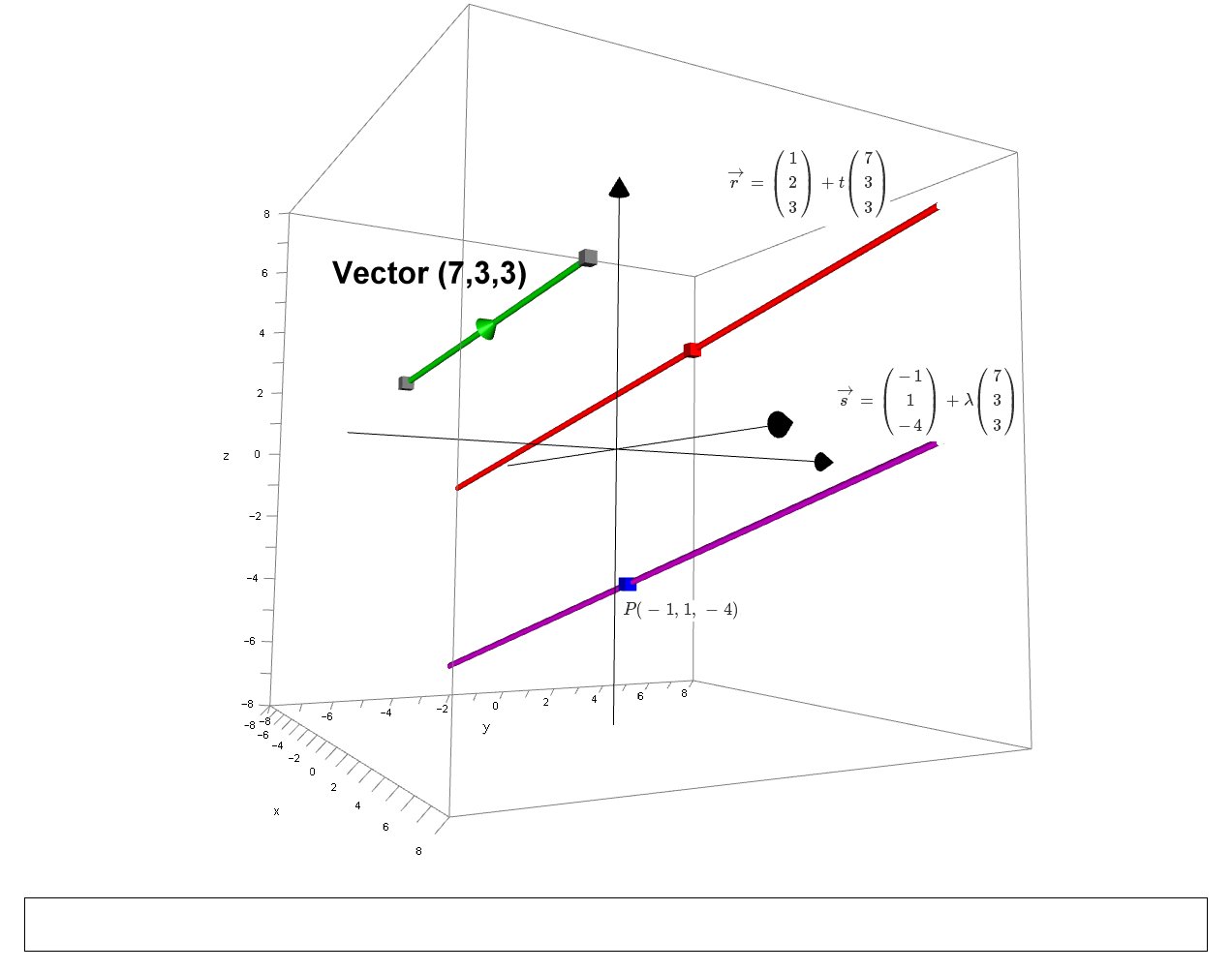
Consider the line which passes through the point P(-1, 1, -4), and which is parallel to the line x=1+7t, y=2+3t, z=3+3t How do you find the point of intersection of this new line with each of the coordinate planes?

Question

34465 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-01-28T15:49:17

#((0),(10/7),(-25/7))#, #((-10/3),(0),(-5))# and #((4/3),(5),(0))#

The vector equation of the line given by:

# x=1+7t; y=2+3t; z=3+3t #

is:

# vec(r) = ((1),(2),(3)) + t((7),(3),(3)) #

So the line is in the direction of the vector #((7),(3),(3)) #

The new line, (whose equation we seek) passes through
#P(-1,1,-4)#, and has the same direction vector, so it has the equation:

# vec(s) = ((-1),(1),(-4)) +lamda((7),(3),(3)) #

enter image source here

So now we need to find the coordinates where this new line, given by #vec(s)# meets the coordinate planes,

For the #x#-axis, #-1+7lamda = 0=> lamda=1/7#, giving

# vec(s) = ((-1),(1),(-4)) +1/7((7),(3),(3)) = ((0),(10/7),(-25/7))#

For the #y#-axis, #1+3lamda = 0=> lamda=-1/3#, giving

# vec(s) = ((-1),(1),(-4)) -1/3((7),(3),(3)) = ((-10/3),(0),(-5))#

For the #z#-axis, #-4+3lamda = 0=> lamda=4/3#, giving

# vec(s) = ((-1),(1),(-4)) +4/3((7),(3),(3)) = ((4/3),(5),(0))#

Hence our coordinates are:

#((0),(10/7),(-25/7))#, #((-10/3),(0),(-5))# and #((4/3),(5),(0))#