Deciding current in a circuit?
Decide #I_1# , #I_2# and #I_3# in the circuit below
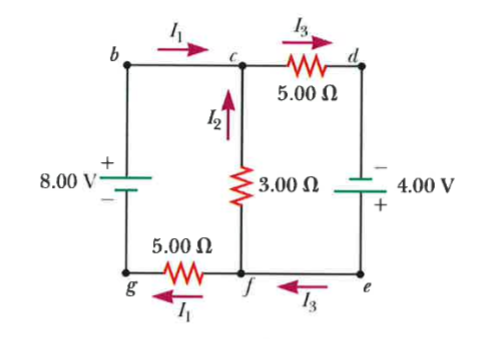
Decide

1 Answer
Explanation:
You can solve the circuit by dividing the effect of the two generators and considering one at a time the effects.
Considering the only battery on the left you have two resistors in parallel on the right
By the value of the resistances, the current in 3 and in 2 caused by V1 are:
Now let's consider only the battery on the right
With the same reasoning, you will have
With the sum of the effects, you have
now you can see that every node is verificated
