Derive elastic strain energy?
How do you derive #E=1/2kx^2# for the elastic strain energy in a deformed material sample obeying Hooke's law?
How do you derive
1 Answer
From Hooke's law,
#vecF = -kvecd# ,where
#vecF# is the restoring force (the force that brings the spring back to equilibrium, and is thus negative),#k# is the force constant, and#vecd# is the positive horizontal displacement from the equilibrium position (defined as zero).
Force is given by units of
Imagine compressing the spring by an infinitesimally small displacement
This switches the sign of
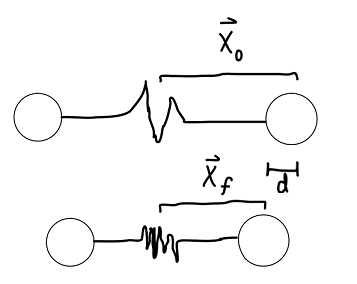
If we integrate the force over a certain compression displacement
#E = int_(vecx_0)^(vecx_f) vecF dvecd#
#= +int_(vecx_0)^(vecx_f) kvecddvecd = +k/2|[vecd^2]|_(vecx_0)^(vecx_f)#
#= k/2 (vecx_f^2 - vecx_0^2)#
Since we defined
If we define
#d^2 = vecx_f^2 - cancel(vecx_0^2)^(0) = (vecx_f - cancel(vecx_0)^(0))^2#
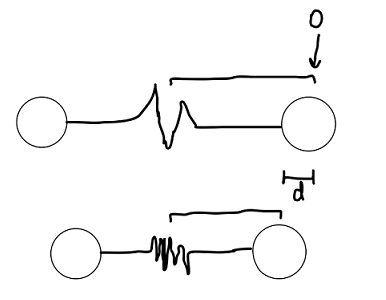
#E = k/2(vecx_f^2)#
#=> color(blue)(E = 1/2kd^2)#
In terms of
#E = 1/2kx^2#

