Does #sin180+sin45=sin225#?
2 Answers
Ehm...I do not think so...
Explanation:
I imagine the arguments in degrees so that if you plot your sin function you get:
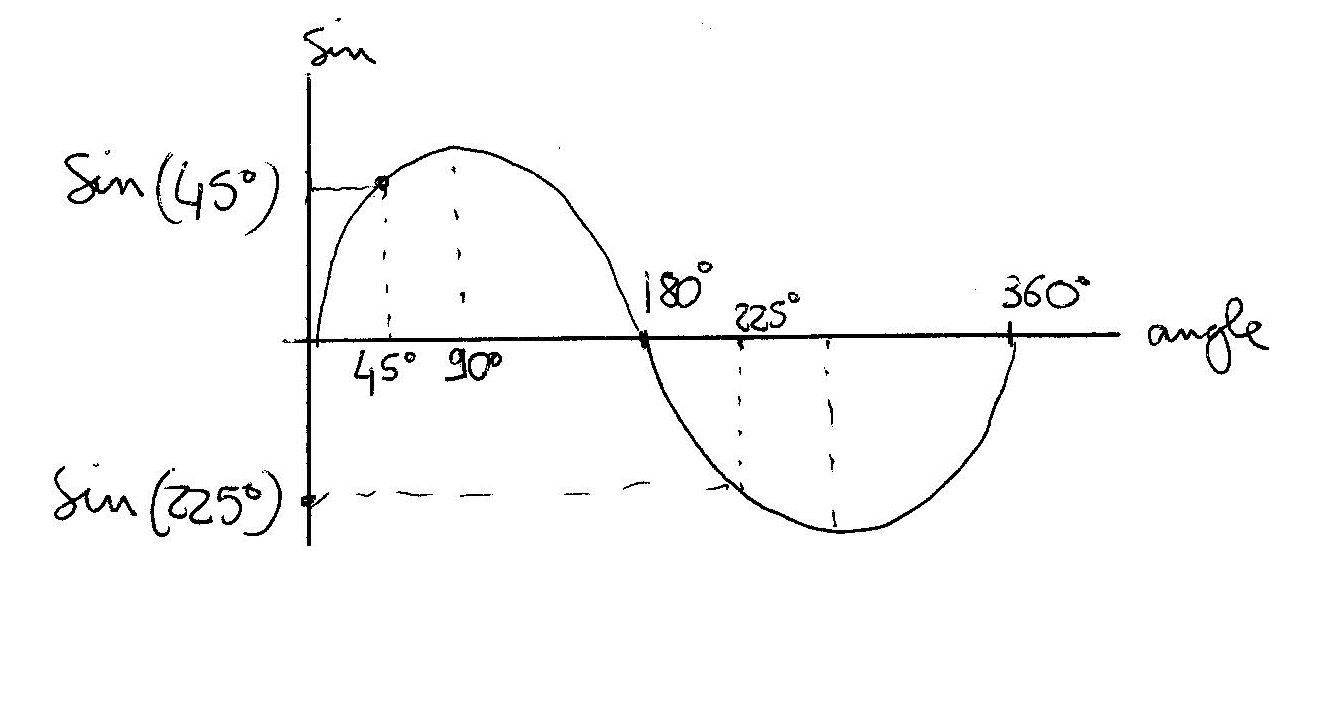
As you can see:
while
I also considered the possibility to have them in radians but it doesn't work either...
No
Explanation:
Remember that taking the
So the
Think of it this way:
#sqrt4 + sqrt25 = sqrt29#
#2+5=sqrt29#
#7cancel(=)sqrt29#
In the same idea,
Like Gio explained, the graphs are also different.
But how can you trust just plain words? Let's actually work out this problem.
#sin180# = 0
#sin(45) = sqrt2/2#
#sin225 = -sqrt2/2#
So:
#sin180 + sin45 = sin225#
#0 + sqrt2/2 cancel(=) -sqrt2/2#
And that's why you cant work with


